Check if all internal nodes of BST have only one child without building tree
Given preorder traversal array for a binary search tree(BST), without actually building the tree check if all internal nodes of BST have only one child.
For example, for the preorder array - {9, 8, 5, 7, 6} the BST would like the tree on the left hand side in below diagram. All its internal nodes have only one child. But for the preorder array - {8, 5, 4, 7, 6} the BST would be the tree shown on the right hand side in below diagram and as you can see node 5 has two children and for this case output returned should be 'false'. 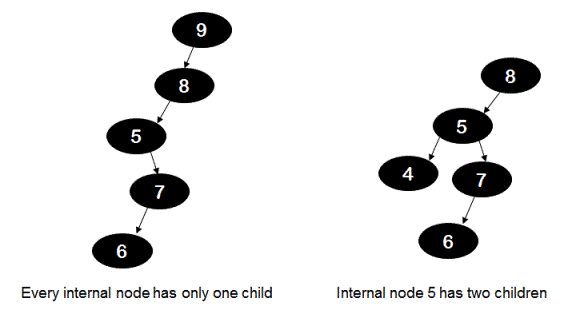
Video coming soon!
Subscribe for more updates
Algorithm/Insights
If a node - 'currentNode' in BST has only one child then that means all the nodes in BST are either in the left sub-tree of that node or in the right sub-tree. This further implies that all nodes would have values either greater than currentNode or all nodes would have values less than currentNode. Therefore in preorder traversal array all elements appearing after the currentNode would all be either greater than currentNode or less than currentNode. If this condition holds true for all elements of preorder array(except the last element: since that would be element for leaf node) then we can say that all internal nodes of BST have only one child.
For example, in the BST constructed using the preorder array {9, 8, 5, 7, 6} all internal nodes have only one child. Now as you can observe,
all elements appearing after 9 are less than 9.
all elements appearing after 8 are less than 8.
all elements appearing after 5 are greater than 5.
all elements appearing after 7 are less than 7.
Now in the algorithm all we need to do is to check if the above condition holds true.
Method 1: For each element preorder[i] starting from i = 0, check if all elements appearing after preorder[i] are either less than or greater than preorder[i]. If for preorder[i], thic conditions holds true then return true else return false. The time complexity for this method would be O(n^2).
Method 2: Now instead of traversing array from index 0, if we start traversing preorder array from index = (size Of preorderArray - 1) towards index = 0, and keep track of maximum and minimum elements seen so far(maxSoFar, minSoFar) then we can easily check if all elements appearing after preorder[i](elements from index i+1 to end) are less than or greater than preorder[i]. If all elements are less than preorder[i] then maxSoFar value must be less than preorder[i] and vice versa.
Please checkout function checkOneChildNodesBST(int[] preorder) in code snippet for implementation details. The time complexity of this algorithm is O(n) with O(1) auxiliary space usage.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Checks if each internal node of BST has only one child without actually building the tree. Runs in O(n) time.
* @author Nilesh
*/
public class OneChildNodesBST
{
private int minimum(int a, int b)
{
if (a < b) return a;
return b;
}
private int maximum(int a, int b)
{
if (a > b) return a;
return b;
}
public boolean checkOneChildNodesBST(int[] preorder)
{
int maxSoFar = preorder[preorder.length - 1], minSoFar = preorder[preorder.length - 1];
/*
* check if all elements in the sub-array from [i+1 to end] of the array
* are less than current element - preorder[i]. If not, all these elements should
* be greater than the current element.
*/
for (int i = preorder.length - 2; i >= 0; i--)
{
if (!((preorder[i] < minSoFar) || (preorder[i] > maxSoFar)))
{
return false;
}
maxSoFar = maximum(preorder[i], maxSoFar);
minSoFar = minimum(preorder[i], minSoFar);
}
return true;
}
public static void main(String[] args)
{
OneChildNodesBST solution = new OneChildNodesBST();
int[] preorderTree1 = {9,8,5,7,6};
int[] preorderTree2 = {8,5,4,7,6};
System.out.println("Check if evry internal node of this BST has only one child:\n" + solution.checkOneChildNodesBST(preorderTree2));
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
