Check if two binary search trees are identical given their array representations
Given two arrays which would be used to construct two different binary search trees(BSTs), write a program to identify if the BSTs constructed from these would be identical. The condition is that the program should be able to identify this without actually building BSTs.
For example, using array {3,5,4,6,1,0,2} the BST constructed would be - 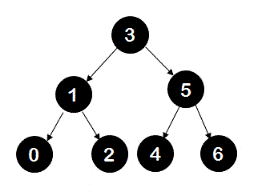
You can verify that using array {3,1,5,2,4,6,0} the same BST would be constructed.
In the following example though, the BST constructed using array {6,9,8} is not same as the BST constructed using array {6,8,9}.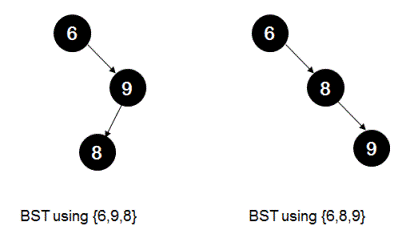
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The idea is to look for the element in both given arrays which would be used to construct the same part of the trees.
For example, given two arrays {3,5,4,6,1,0,2} and {3,1,5,2,4,6,0}; in both of these arrays element 3 would be used to construct the root of the tree. Now in both of these arrays, if we search for an element which would be used to construct the root of the right sub-tree of node '3' then that element would turn out to be 5. The reason for this is that both of these arrays, element 5 is the first element found which is greater than 3. Similarly, if we search for an element which would be used to construct the root of the left sub-tree of node '3', that element would be 1. This is because element 1 is the first element found in both of these arrays which is less than 3. Until this point we know that for both of these BSTs - root 3, and it's left and right sub-tree roots(node 1 and node 5 respectively) are same. Moving ahead, to construct root of the left sub-tree of node '5', we look for the first element which is less than 5 but greater than 3. The first such element found in both of the arrays is 4. Similarly, to construct the root of the right sub-tree of node '1', we look for the first element in array which is greater than 1 but less than 3. Using this ides we check for equality of elements in two arrays corresponding to identical parts of the BSTs and we check this for all possible parts of BSTs using recursion.
Please check function checkIfSameBSTs(int[] arrayForTree1, int[] arrayForTree2, int index1, int index2, int min, int max) which has more comments to help understand the implementation details.
Time complexity of this algorithm is O(n^2) in worst case.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Checks if identical BSTs without building them in time O(n^2).
* @author Nilesh
*/
public class CheckIdenticalBSTs
{
private boolean checkIfSameBSTs(int[] arrayForTree1, int[] arrayForTree2, int index1, int index2, int min, int max)
{
/*
* find the first element between min and max.
* that element would be used as the root of the subtree we are looking to construct
*/
int i,j;
for (i = index1; i < arrayForTree1.length; i++)
{
if ((min < arrayForTree1[i]) && (arrayForTree1[i] < max))
{
break;
}
}
for (j = index2; j < arrayForTree2.length; j++)
{
if ((min < arrayForTree2[j]) && (arrayForTree2[j] < max))
{
break;
}
}
/*
* since we are constructing same part of the trees for both arrays
* element found should be same. If element not found,
* then that means we found no node satisfying this condition.
* If this is the case then this should be the case for both the trees
*/
if ((i == arrayForTree1.length) && (j == arrayForTree2.length))
{
return true; // no node found for both trees
}
if ((i == arrayForTree1.length) || (j == arrayForTree2.length))
{
return false; // no node found only in case of one of the trees
}
// if current nodes are same then check if left and right sub-trees for current nodes are same
if (arrayForTree1[i] == arrayForTree2[j])
{
return (checkIfSameBSTs(arrayForTree1, arrayForTree2, i+1, j+1, min, arrayForTree1[i]) &&
checkIfSameBSTs(arrayForTree1, arrayForTree2, i+1, j+1, arrayForTree1[i], max));
}
return false;
}
public boolean checkIfSameBSTs(int[] arrayForTree1, int[] arrayForTree2)
{
return checkIfSameBSTs(arrayForTree1, arrayForTree2, 0, 0, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
public static void main(String[] args)
{
CheckIdenticalBSTs solution = new CheckIdenticalBSTs();
int[] arrayForTree1 = {3,5,4,6,1,0,2};
int[] arrayForTree2 = {3,1,5,2,4,6,0};
System.out.println("Check if identical BSTs: " + solution.checkIfSameBSTs(arrayForTree1, arrayForTree2));
}
}
Order of the Algorithm
Time Complexity is O(n^2)
Space Complexity is O(1)
