Check if the given n-ary tree is symmetric tree or not
Write a program to check if the given n-ary tree is symmetric tree or not. A symmetric tree is defined as a tree which is mirror image of itself about the root node. For example, following tree is a symmetric tree.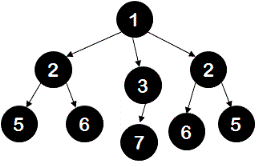
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The algorithm is an implementation of a simple idea that -
1. For given two trees, if both trees are empty then they are mirror images of one another.
Else they have to satisfy following conditions:
2. Root values of both trees have to be same. This can be checked by comparing values of root nodes for given two trees.
3. Sub-tree rooted at the first position should be mirror image of sub-tree rooted at the last position, sub-tree rooted at second position should be mirror image of the sub-tree rooted at second last-position and so on. This can be checked by making recursive calls.
Initial call to checkSymmetry(TreeNode root1, TreeNode root2) is made with root1 = root and root2 = root.
This algorithm is similar to the algorithm for solving the problem - Check if a given binary tree is symmetric or not.
Time complexity of this algorithm is O(n) since in the worst case each node need to be visited once.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution to check if n-ary tree is symmetric or not. Uses Pre-order traversal.
* @author Nilesh
*/
public class CheckIfSymmetricNaryTree
{
class TreeNode
{
private int data;
ArrayList<TreeNode> children;
public TreeNode(int data)
{
this.data = data;
children = new ArrayList();
}
}
private TreeNode root;
/*
* Create a sample tree
* 1
* 2 3 2
* 5 6 7 6 5
*
*/
public void createSampleTree()
{
TreeNode n1 = new TreeNode(1);
TreeNode n20 = new TreeNode(2);
TreeNode n21 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n50 = new TreeNode(5);
TreeNode n51 = new TreeNode(5);
TreeNode n60 = new TreeNode(6);
TreeNode n61 = new TreeNode(6);
TreeNode n70 = new TreeNode(7);
TreeNode n71 = new TreeNode(7);
root = n1;
root.children.add(n20);
root.children.add(n3);
root.children.add(n21);
n20.children.add(n50);
n20.children.add(n60);
n21.children.add(n61);
n21.children.add(n51);
n3.children.add(n70);
}
public boolean checkSymmetry(TreeNode root1, TreeNode root2)
{
if (root1 == null && root2 == null)
{
return true;
}
else if (root1 == null || root2 == null)
{
return false;
}
else if (root1.data == root2.data)
{
int i = 0, j = root2.children.size() - 1;
while ((i < root1.children.size()) && (j >= 0))
{
if (!checkSymmetry(root1.children.get(i), root2.children.get(j)))
{
break;
}
i++; j--;
}
if ((i < root1.children.size()) || (j >= 0))
{
return false;
}
else
{
return true;
}
}
return false;
}
public static void main(String[] args) {
CheckIfSymmetricNaryTree tree = new CheckIfSymmetricNaryTree();
/*
* Create a sample tree
* 1
* 2 3 2
* 5 6 7 6 5
*
*/
tree.createSampleTree();
System.out.print("If given n-ary tree is symmetric tree: " + tree.checkSymmetry(tree.root, tree.root));
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
