Convert binary tree to binary search tree
Convert the given binary tree to binary search tree(BST) without changing the spatial structure of given binary tree. For example, in the below diagram tree on the left hand side is converted to BST on right hand side while maintaining the original spatial structure of binary tree.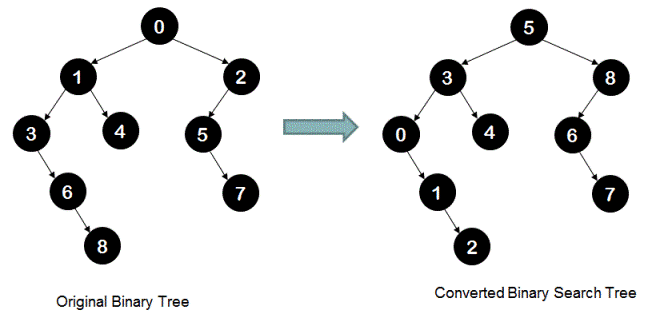
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The algorithm uses following simple steps to solve this problem.
1. It creates the inorder traversal array of a given binary tree.
2. Then it sorts the created inorder array.
3. Now it again traverses given binary tree in inorder fashion and simultaneously it traverses sorted inorder array. At each node visit of binary tree, the value of that node is changed to corresponding element in the inorder array. That is value of first node visited during inorder traversal is changed to value of element at 0th index in sorted inorder array, value of second node visited during inorder traversal is changed to value of element at 1st index and so on.
You may want to checkout function changeTreeToBST() for implementation details.
In the above algorithm, Step #1 and #3 take O(n) time and step #2 which is a sorting step takes O(nlogn) time using heap sort/merge sort method. Therefore, overall time complexity of this method is O(nlogn).
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.Arrays;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Converts the given binary tree to binary search tree
* while maintaining the spatial structure of original binary tree.
* @author Nilesh
*/
public class ConvertBinaryTreeToBST
{
class QueueNode
{
TreeNode treeNode;
int level;
QueueNode(TreeNode node, int level)
{
this.treeNode = node;
this.level = level;
}
}
class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
int treeSize;
/*
0
1 2
3 4 5
6 7
8
*/
private TreeNode createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.right = n6;
n5.right = n7;
n6.right = n8;
treeSize = 9;
return root;
}
public void printTreeLevelOrder()
{
if (root == null) return;
LinkedList queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentNode = (QueueNode) queue.remove();
if (currentNode.level > maxLevelVisited)
{
maxLevelVisited = currentNode.level;
System.out.print("\nlevel-" + currentNode.level + " nodes: ");
}
System.out.print(" " + currentNode.treeNode.value);
if (currentNode.treeNode.left != null)
{
queue.add(new QueueNode(currentNode.treeNode.left, currentNode.level + 1));
}
if (currentNode.treeNode.right != null)
{
queue.add(new QueueNode(currentNode.treeNode.right, currentNode.level + 1));
}
}
}
private void createInorderArray(TreeNode currentNode, int[] inorder, int[] index)
{
if (currentNode == null)
{
return;
}
createInorderArray(currentNode.left, inorder, index);
inorder[index[0]] = currentNode.value;
index[0] += 1;
createInorderArray(currentNode.right, inorder, index);
}
private void changeNodeValues(TreeNode currentNode, int[] inorder, int[] index)
{
if (currentNode == null)
{
return;
}
changeNodeValues(currentNode.left, inorder, index);
currentNode.value = inorder[index[0]];
index[0] += 1;
changeNodeValues(currentNode.right, inorder, index);
}
public void changeTreeToBST()
{
int[] inorder = new int[treeSize];
int[] index = new int[1];
// creates inorder array from original tree
createInorderArray(root, inorder, index);
Arrays.sort(inorder);
// reset index into inorder array
index[0] = 0;
// modifies tree by changing node values while traversing tree in inorder fashion
changeNodeValues(root, inorder, index);
}
public static void main(String[] args)
{
ConvertBinaryTreeToBST solution = new ConvertBinaryTreeToBST();
/*
0
1 2
3 4 5
6 7
8
*/
solution.createTree();
solution.changeTreeToBST();
System.out.print("Modified tree to BST: \n");
/*
5
3 8
0 4 6
1 7
2
*/
solution.printTreeLevelOrder();
}
}
Order of the Algorithm
Time Complexity is O(nlogn)
Space Complexity is O(n)
