Diagonal Sum of a Binary Tree.
Consider lines drawn at an angle of 135 degrees(that is slope = -1) which cut through the left branches of a given binary tree. A diagonal is formed by nodes which lie between two such consecutive lines. If we are able to draw 'n' lines then the complete tree is divided into 'n+1' diagonals. Diagonal sum in a binary tree is sum of all node's values lying between these lines. Given a binary tree, print all diagonal sums. Please note that all right branches are drawn parallel to each other and all left branches are also drawn parallel to each other.
For example,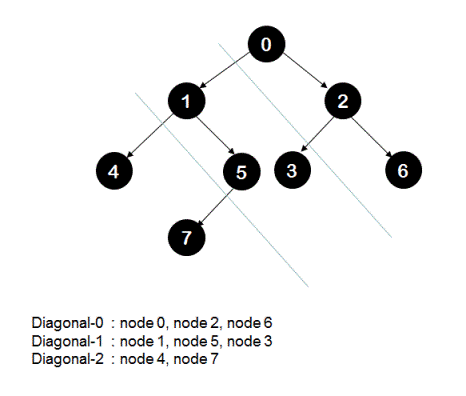
in the above tree there are total of three diagonals.
Diagonal-0 has 3 nodes in it: node-0, node-2 and node-6. Therefore, sum of all nodes in diagonal-0 is 8.
Similarly, sum of nodes in diagonal-1 is 9(node-1, node-5 and node-3). And sum of nodes in diagonal-2 is 11(node-4, node-7).
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
Please observe below tree carefully. 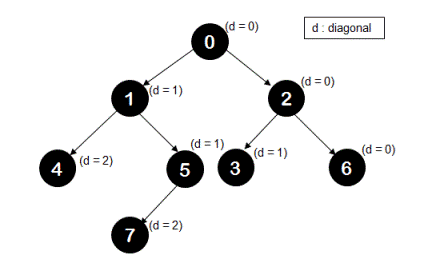
As is marked in the tree, root node-0 is placed in diagonal 0, then its left child node-1 is placed in diagonal 1 and its right child node-2 is placed in the same diagonal as node-0 that is diagonal 0. This observation can be easily generalized - if current node is placed in diagonal 'd' then its left child would be placed in diagonal 'd+1' and its right child would be placed in the same diagonal as that of current node that is diagonal 'd'.
Now using above insight, we can easily find the diagonal in which a node is placed in and then add that node's value to that diagonal.
We traverse the complete tree using inorder traversal starting from the root node. During this traversal, we pass the 'currDiag' to each node indicating which diagonal that current node is placed in. We start by passing 'currDiag = 0' for the root node. Each node passes down 'currDiag + 1' to its left child and 'currDiag' to its right child. Now using this 'currDiag' value, we add current node to appropriate diagonal's sum. To store diagonal sum for each diagonal separately, HashMap is used with its key as diagonal number and value as sum of nodes in that diagonal.
Time complexity of this algorithm is O(n) since each node would be visited once. Space complexity in the worst case would be O(n). Worst case space complexity occurs for the skewed tree where right child for each node is null. Average case space complexity of this algorithm would be O(log(n)).
Please check out the function 'computeDiagSum(TreeNode currentNode, int currDiag, HashMap
Feel free to add comments below in case you have any queries/feedback.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Computes sum of nodes in each diagonal using inorder traversal.
* @author Nilesh
*/
import java.util.HashMap;
import java.util.Map;
public class DiagonalSumTree
{
private class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
0
1 2
4 5 3 6
7
*/
public void createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
root.left = n1;
root.right = n2;
n1.left = n4;
n1.right = n5;
n2.left = n3;
n2.right = n6;
n5.left = n7;
}
private void computeDiagSum(TreeNode currentNode, int currDiag, HashMap<Integer, Integer> diagSum)
{
if (currentNode == null)
{
return;
}
// compute diagonal sum for the tree rooted at the left child
// left child would be placed in 'currDiag + 1'
computeDiagSum(currentNode.left, currDiag + 1, diagSum);
// now add current node's value to its diagonal sum
int prevSum = (diagSum.get(currDiag) == null) ? 0 : diagSum.get(currDiag) ;
diagSum.put(currDiag, prevSum + currentNode.value);
// compute diagonal sum for the tree rooted at the right child
// right child would be placed in the same diagonal as that of current node
computeDiagSum(currentNode.right, currDiag, diagSum);
}
public void computeDiagSum(HashMap<Integer, Integer> diagSum)
{
computeDiagSum(root, 0, diagSum);
}
public static void main(String[] args)
{
DiagonalSumTree solution = new DiagonalSumTree();
/*
0
1 2
4 5 3 6
7
*/
solution.createTree();
HashMap<Integer, Integer> diagSum = new HashMap();
// this call populates diagSum HashMap with sum for all diagonals
solution.computeDiagSum(diagSum);
// print sum for each diagonal
for (Map.Entry<Integer, Integer> entry : diagSum.entrySet())
{
System.out.println("Diagonal Sum for level " + entry.getKey() + " :" + entry.getValue());
}
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
