Maximum size square sub-matrix with all 1s
Given a matrix of dimensions mxn having all entries as 1 or 0, find out the size of maximum size square sub-matrix with all 1s.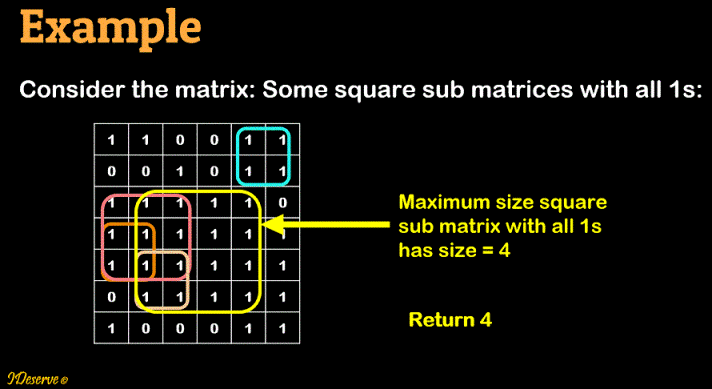
Please check out the video below for detailed explanation of the algorithm with animations.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
Step 1: Create an empty table of size mxn, defined as
table[i][j] = Size of maximum square sub matrix with all 1s with matrix[i][j] as bottom right element.
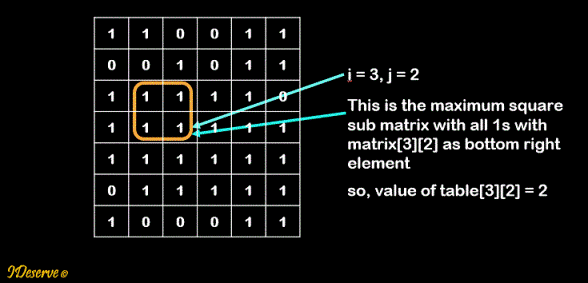
Step 2: Set values in table based on the conditions
a. if i = 0 or j = 0, table[i][j] = matrix[i][j]
b. else if matrix[i][j] = 0 then table[i][j] = 0
c. else table[i][j] = min(table[i - 1][j - 1], table[i - 1][j], table[i][j - 1]) + 1;
During step 2, maintain largest element added in the table and finally return it.
Please check out the video above for detailed explanation of the algorithm with animations.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given a matrix of dimensions mxn having all entries as 1 or 0,
* find out the size of maximum size square sub-matrix with all 1s.
*
* @author Saurabh
*/
public class MaximumSizeSquareSubmatrixWithAllOnes {
private static int maximumSizeSquareSubmatrixWithAllOnes(int[][] matrix) {
int maxSize = 0;
int r = matrix.length;
int c = matrix[0].length;
// Step 1
int[][] table = new int[r][c];
for (int i = 0; i < r; i++) {
for (int j = 0; j < c; j++) {
// Step 2 a
if (i == 0 || j == 0) {
table[i][j] = matrix[i][j];
maxSize = table[i][j] > maxSize ? table[i][j] : maxSize;
}
// Step 2 b
else if (matrix[i][j] == 0) {
table[i][j] = 0;
}
// Step 2 c
else {
table[i][j] = min(table[i - 1][j - 1], table[i - 1][j], table[i][j - 1]) + 1;
maxSize = table[i][j] > maxSize ? table[i][j] : maxSize;
}
}
}
return maxSize;
}
private static int min(int i, int j, int k) {
return i <= j && i <= k ? i : (j <= i && j <= k ? j : k);
}
public static void main(String[] args) {
int matrix[][] = { { 1, 1, 0, 0, 1, 1 },
{ 0, 0, 1, 0, 1, 1 },
{ 1, 1, 1, 1, 1, 0 },
{ 1, 1, 1, 1, 1, 1 },
{ 1, 1, 1, 1, 1, 1 },
{ 0, 1, 1, 1, 1, 1 },
{ 1, 0, 0, 0, 1, 1 }
};
System.out.println(maximumSizeSquareSubmatrixWithAllOnes(matrix));
}
}
Order of the Algorithm
Time Complexity is O(mn)
Space Complexity is O(mn)
