Set Partition Problem | Dynamic Programming
In one of the previous posts, we have looked at the recursive solution for set partitioning problem. In this post, we will cover the dynamic programming approach to solve the same problem. If you have already read the previous post with recursive solution, you can directly skip to 'Algorithm/Insights' section.
Given a set, find out if it can be partitioned into two disjoint subsets such that sum of the elements in both these subsets is equal. Intersection of disjoint sets should be null and union should be the complete set.
For set {7,5,3,5}, sets {7,5} and {3,5} are valid disjoint sets. Also sets {7,5,3,5} and {} are valid disjoint sets. But sets {7,5,3} and {3,5} are not valid disjoint sets since element 3 is present in both of these subsets.
Coming back to the problem of finding two disjoint sets with equal sums, an example for that could be subsets {7,3} and {5,5} for set {7,5,3,5}. Sum of elements in both of these subsets is 10. Therefore, the output returned by the program should be 'True'.
Output returned by the program should be 'false' for the set {21,33,37,2}. You can verify that, this set cannot be partitioned into any valid combination of two disjoint subsets such that sum of elements in these subsets is equal.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
If sum of all the elements in the given set is an odd number say '2n+1', then the best we might be able to do is to partition the given set into two subsets - one with sum 'n' and another with sum 'n+1'. In other words, if sum of all the elements in given set is odd, there is no way the set can be partitioned into two subsets with equal sum and therefore we return 'false' in this case.
Now if the sum of all the elements in the given set is an even number say '2n', then all we need to do is to find out a subset say 'S1' of the given set such that sum of elements in that subset is 'n'. The remaining subset(obtained by excluding elements in 'S1') then is guaranteed to have sum = 'n'. For example, the sum of all elements for this set {15,5,15,20,45} is 100. And the subset {5,45} has sum = 50. Now the remaining subset obtained by excluding elements 5 and 45 is {15,15,20} which also has sum = 50.
Notice how we have reduced the original problem into the problem of finding a subset with sum = 'n' when sum of all elements in given set is '2n'. Let's try to solve this modified problem now.
We are going to use dynamic programming(tabulation) approach to solve this problem. We will fill up the 'solution' array shown below in bottom up manner.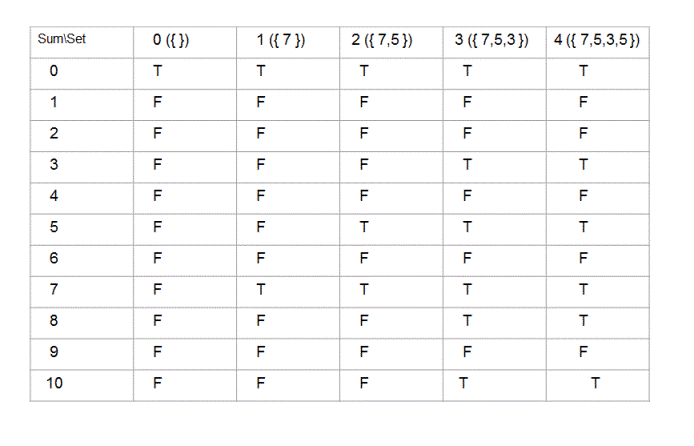
Here, value of solution[i][j] represents if sum of 'i' could be obtained by any subset of the set having first 'j' elements (from the given set) in it. For example, for the set {7,5,3,5} solution[8][3] would be 'true' since sum of 8 could be obtained by a subset({5,3}) of the set {7,5,3}(set obtained by considering first 3 elements of the given set).
Here is how we fill up this solution array -
Initialization:
1. All elements in 0th row are initialized to 'true' because for any given set, we can always find an empty subset with sum = '0'
2. All elements in 0th column except the element in the 0th row are initialized to 'false' since no sum except 0 could be obtained by any subset of the empty set({}).
Rules for filling up solution[i][j]:
1. If solution[i][j-1] is 'true' then solution[i][j] is also 'true'. This is because if there exists a subset(with sum = 'i') of set formed by first 'j-1' elements(of given set) then that same subset will also be a subset for the set formed by first 'j' elements.
2. If solution[i][j-1] is 'true' then solution[(i + set[j-1])][j] is also 'true'. This is because if there exists a subset(with sum = 'i') of set formed by first 'j-1' elements(of given set) then inserting 'j'th element into that subset results in a new subset which will have sum = 'i' + value of 'j'th element. This sum is represented by the row = 'i + set[j-1]'. Remember indexing scheme used here is 0 based and therefore value of 'j'th element is represented by set[j-1].
3. If solution[i][j] is not set to 'true' using above two rules then set solution[i][j] to 'false'. Because there is no other case other than above two cases in which solution[i][j] would be 'true'.
Using above two rules and initialization, function 'partitionPossible(int requiredSum, int[] set)' fills up 'solution' array in bottom up manner as shown below.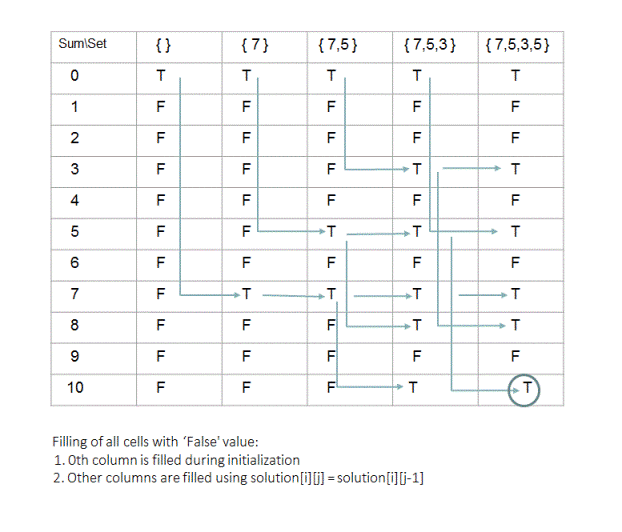
Return value: Note that if we are looking for a subset of the given set with sum = 'requiredSum' then number of rows(numRows) for above 'solution' array would be 'requiredSum + 1' and number of columns(numCols) would be 'size of given set + 1'. Once we fill up this 'solution' array, we need to return the value of solution[numRows-1][numCols-1].
Please check out the code snippet for implementation details. The time complexity of this approach is O(nm) where size of the given set is 'm' and sum of all elements in the given set is '2n'. The auxillary space required is also O(nm).
Feel free to add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Iterative polynomial solution to find out if given set can be partitioned into two disjoint subsets such that -
* sum of the elements in both these subsets is equal.
* Uses dynamic programming with tabulation approach.
* @author Nilesh
*/
public class PartitionProblem
{
private boolean partitionPossible(int requiredSum, int[] set)
{
// each column indicates the set we are looking at and each row indicates the sum we are looking for
boolean[][] solution = new boolean[requiredSum + 1][set.length + 1];
int numRows = requiredSum + 1, numCols = set.length + 1;
// we can always find an empty subset with sum = 0
for (int j = 0; j < numCols; j++)
{
solution[0][j] = true;
}
// no sum except 0 could be obtained using an empty subset
for (int i = 1; i < numRows; i++)
{
solution[i][0] = false;
}
for (int j = 1; j < numCols; j++)
{
for (int i = 0; i < numRows; i++)
{
/*
* Rule 1 - If solution[i][j-1] is 'true' then solution[i][j] is also 'true'. This is because -
* if there exists a subset(with sum = 'i') of set formed by first 'j-1' elements (of given set)
* then that same subset will also be a subset for the set formed by first 'j' elements.
*
* Rule 2 - If solution[i][j-1] is 'true' then solution[(i + set[j-1])][j] is also 'true'.
* This is because if there exists a subset(with sum = 'i') of set formed by first 'j-1' elements
* (of given set) then inserting 'j'th element into that subset results in a new subset
* which will have sum = 'i' + value of 'j'th element. This sum is represented by the row = 'i'+set[j-1]'.
* Remember indexing scheme used here is 0 based and therefore value of 'j'th element
* is represented by set[j-1].
*/
if (solution[i][j-1] == true)
{
solution[i][j] = true;
if (((i + set[j-1]) < numRows))
{
solution[(i + set[j-1])][j] = true;
}
}
/*
* If solution[i][j] is not set to 'true' using above two rules
* then set it to 'false'. Because there is no other case other than
* above two cases in which solution[i][j] would be 'true'.
*/
else if (solution[i][j] != true)
{
solution[i][j] = false;
}
}
}
// see if the 'requiredSum' could be obtained by any subset of the given set
return solution[numRows-1][numCols-1];
}
public boolean partitionExists(int[] set)
{
int sum = 0;
for (int i = 0; i < set.length; i++)
{
sum += set[i];
}
/*
* if sum of all the elements in given set is odd,
* there is no way they can be partitioned to have equal sum for both partitions
*/
if ((sum % 2) != 0)
{
return false;
}
// else we just need to find a subset which has sum = (sum of all elements in the set)/2
return partitionPossible(sum/2, set);
}
public static void main(String[] args)
{
PartitionProblem solution = new PartitionProblem();
int[] set = {7, 5, 3, 5};
System.out.println(solution.partitionExists(set));
}
}
Order of the Algorithm
Time Complexity is O(nm) where m: size of the given set, 2n: sum of all elements in the given set.
Space Complexity is O(nm)
