AVL tree | Basics
In this article, we will cover general concepts about AVL trees without going into the implementation details. In following articles, we have covered implementation details of AVL tree.
Implementation for AVL tree insertion.
Implementation for AVL tree deletion.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
What is AVL tree?
AVL tree is a type of binary search tree in which at any given node, absolute difference between heights of left sub-tree and right sub-tree cannot be greater than 1. This property of the AVL tree helps to keep the tree height balanced. Let's look at following examples to understand the definition of the AVL tree.
In the following example, leftmost tree which has only one node '5' is an AVL tree because for this node '5', height of the left sub-tree is 0 and height of the right sub-tree is also 0, hence the difference between heights of left and right sub-trees is not greater than 1.
The middle tree with two nodes - node '5' and node '4' is also an AVL tree. For node '4', height of both left and right sub-tree is 0. For node '5', height of left sub-tree is '1' and height of right sub-tree is 0.
Now the rightmost tree is not an AVL tree because for node '5', height of the left sub-tree is 2 and height of right sub-tree is 0 which makes the difference between height of left sub-tree and right sub-tree greater than 1.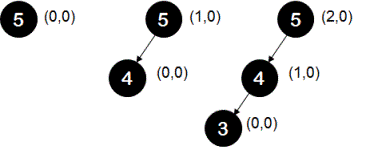
Note that we are looking at absolute difference between heights. The following tree is also not an AVL tree because at node '3', difference between height of left sub-tree and right sub-tree is greater than 1.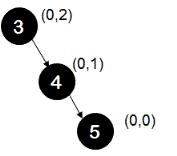
Similarly, you can confirm that following tree is an AVL tree.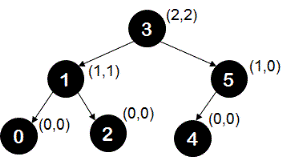
Why is it used?
In case of a normal binary search tree(BST), average time complexity for insert, search and delete operations is O(logn). But worst case time complexity for these operations for BST is O(n). This worst case occurs when the BST formed is skewed one similar to below shown BST. 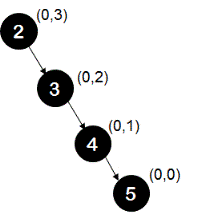
With an AVL tree, because the BST will always be height balanced, even the worst case time complexity for insert, search and delete operations is O(logn).
How exactly AVL tree maintains its height balance?
An AVL tree maintains its height balance by performing rotation operations if any of the nodes violate the AVL tree property of height balance(difference of heights for left and right sub-tree greater than 1). Let's now look at the examples to understand height balance using rotations.
Example-1: For the following tree, AVL tree property is violated at node '5'. 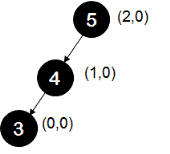
The height of the left sub-tree is greater than the height of the right sub-tree by 2. This difference of 2 is contributed by two left branches - branch 5-4 and branch 4-3. If the difference of 2 is contributed by two left branches then we call this case a left-left case. In this case, we perform a right rotation as shown below. Notice how even after performing the rotation, the BST property is maintained.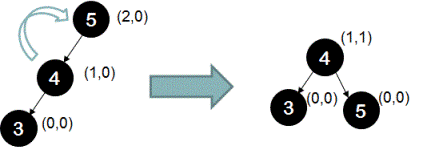
Example-2: For the following tree, AVL tree property is violated at node '8'.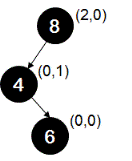
The height of the left sub-tree is greater than the height of the right sub-tree by 2. This difference of 2 is contributed by one left branch(branch 8-4) and one right branch(branch 4-6). If the difference of 2 is contributed in such a way that one of them is the left branch originating from the node at which height balance is violated(node '8' in this case) and remaining contributing branch is the right branch, then we call this case as left-right case. To restore height balance in this case, we first perform a left rotation followed by a right rotation as shown below.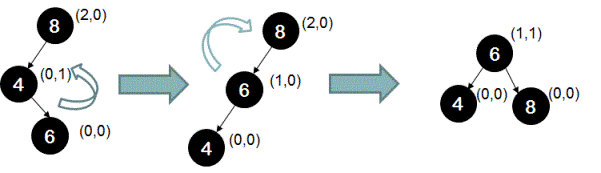
The following two examples are structural mirror images of above two examples.
Example-3: This is the right-right case and is structural mirror image of example-1. 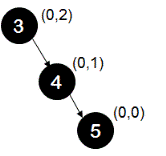
To restore the balance, we need to perform left rotation as shown below.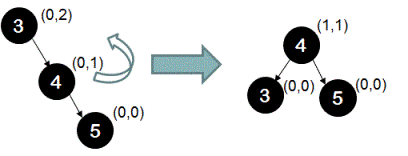
Example-4: This is the right-left case and is structural mirror image of example-2. 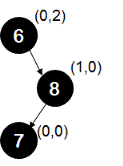
To restore the balance, we need to perform right rotation followed by left rotation as shown below.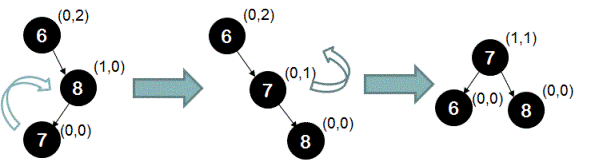
In general, right rotation operation at 'node' is performed as following. 
Notice how the order of keys that is - keys(T1) < 'beta' < keys(T2) < 'node' < keys(T3) is maintained even after the rotation.
And left rotation operation at 'node' is performed as following. 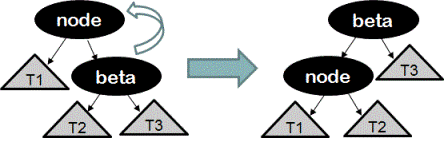
Notice how the order of keys that is keys(T1) < 'node' < keys(T2) < 'beta' < keys(T3) is maintained even after the rotation.
Order of the Algorithm
Time Complexity is O(logn)
