Find total number of ways to make change using given set of coins
Given an infinite supply of coins of denominations {20,10,5,1}, find out total number of way to make change of given amount - 'n'?
For example, if given amount is 20, there are 10 ways to make this change as shown below -
(1 of 20),(1 of 10 + 2 of 5),(1 of 10 + 1 of 5 + 5 of 1),(1 of 10 + 10 of 1), (2 of 10), (1 of 5 + 15 of 1),(2 of 5 + 10 of 1),(3 of 5 + 5 of 1),(4 of 5),(20 of 1)
If the amount given is 0 then the total number of ways to make change is 1 - using 0 coins of every given denomination.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Let's try to understand this algorithm using an example. If we are make change of 50 using infinite number of coins of denominations {20,10,5,1} then
total number of ways to make change of 50 using denominations {20,10,5,1} = total number of ways to make change of 50 using 0 coins of 20 + total number of ways to make change of 50 using 1 coin of 20 + total number of ways to make change of 50 using 2 coins of 20
Now first term on the right hand side of above equation that is - total number of ways to make change of 50 using 0 coins of 20 can be restated as total number of ways to make change of 50 using denominations {10,5,1}
And second term that is total number of ways to make change of 50 using 1 coin of 20 = total number of ways to make change of 30 using denominations {10,5,1}
Similarly, total number of ways to make change of 50 using 2 coins of 20 = total number of ways to make change of 10 using denominations {10,5,1}.
As you can see, this algorithm is recursive in nature and the recursion tree for the above example looks like following. Only one complete path is shown in recursion tree due to space constraint.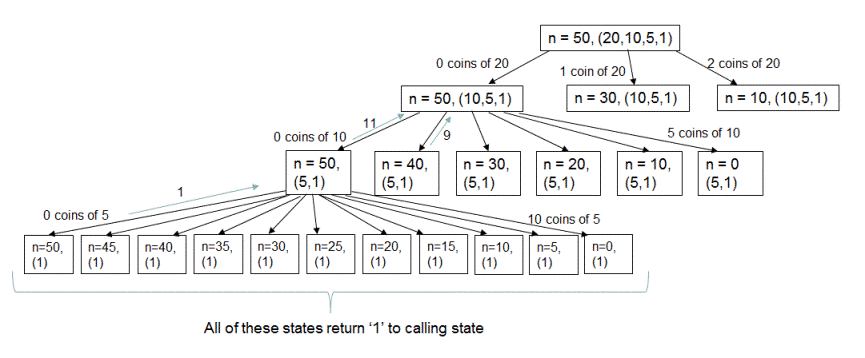
The base case for this algorithm would be when the denomination set has only coins of 1 in it. In that case total number of ways to make change would be 1. Also when amount to make change of is 0, total number of ways to make change would be 1(0 coins of all denominations).
The formal steps of this algorithm are -
1. If the current denomination is 1 then return 1. This is the base case.
2. If current denomination is 20, set next denomination as 10; if current denomination is 10, set next denomination as 5 and if current denomination is 5, set next denomination as 1.
3. Now implement the recurrence relation: numberOfWays(amount, denom) = numberOfWays(amount - 0*denom, nextDenom) + numberOfWays(amount - 1*denom, nextDenom) + ... + numberOfWays(0, nextDenom) using a while loop.
The time complexity of this algorithm is exponential as can be easily observed from recursion tree.
Dynamic Programming - Memoization approach: For the same example, if we look at the recursion tree shown below which highlights the re-computations for the sub-problems of n = 30 and denominations = {5,1}, n = 20 and denominations = {5,1} and so on.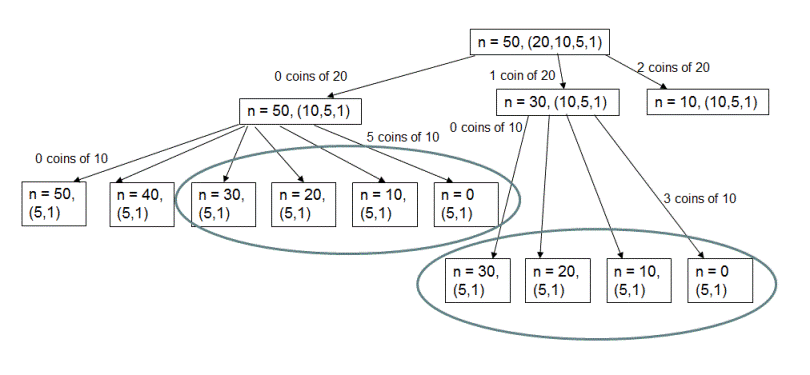
To avoid these re-computations, we could store the results when computed and re-use them if required again. This reduces the time complexity of this algorithm to O(nm) where n is total amount to make change for and m is total number of denominations. For the example shown in the recursion tree n would be 50 and m would be 4. This approach takes extra space of O(nm). Please checkout function countNumberOfWays(int amount, int denom, HashMap
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Total number of ways to make change using an infinite supply of coins of denomination set {20,10,5,1}
* @author Nilesh
*/
import java.util.HashMap;
import java.util.Objects;
public class WaysOfMakingChange
{
class AmountDenom
{
int amount;
int denom;
public AmountDenom(int amount, int denom)
{
this.amount = amount;
this.denom = denom;
}
// we need to override hashCode and equals method for user defined objects when these objects are used as keys
@Override
public int hashCode()
{
// since this code uses jdk 7
return Objects.hash(this.amount, this.denom);
}
@Override
public boolean equals(Object obj){
if (obj instanceof AmountDenom) {
AmountDenom keyObj = (AmountDenom) obj;
return (keyObj.amount == this.amount && keyObj.denom == this.denom);
} else {
return false;
}
}
}
// denominations we can use : 20,10,5 and 1
public int countNumberOfWays(int amount, int denom, HashMap<AmountDenom, Integer> numberOfWays)
{
// if only denominations available is 1 then number of ways to make change = 1
if (denom == 1)
{
// store the computed result for re-use
numberOfWays.put(new AmountDenom(amount, denom), 1);
return 1;
}
int nextDenom = 0;
if (denom == 20) // if current denom is 25 then next denom to be used is 10
{
nextDenom = 10;
}
else if (denom == 10) // if current denom is 10 then next denom to be used is 5
{
nextDenom = 5;
}
else if (denom == 5) // if current denom is 5 then next denom to be used is 1
{
nextDenom = 1;
}
// try all possible number of coins of current denomination
int numberOfCoins = 0, ways = 0, modifiedAmount;
while ((numberOfCoins*denom) <= amount)
{
modifiedAmount = amount - (numberOfCoins*denom);
// check if we have already computed the number of ways for this amount and denom set
if (numberOfWays.get(new AmountDenom(modifiedAmount, denom)) != null)
{
ways += numberOfWays.get(new AmountDenom(modifiedAmount, denom));
}
else
{
ways += countNumberOfWays(modifiedAmount, nextDenom, numberOfWays);
}
numberOfCoins += 1;
}
// store the computed result for re-use
numberOfWays.put(new AmountDenom(amount, denom), ways);
return ways;
}
// denominations we can use : 20,10,5 and 1
public int countNumberOfWays(int amount, int denom)
{
// if only denominations available is 1 then number of ways to make change = 1
if (denom == 1)
{
return 1;
}
int nextDenom = 0;
if (denom == 20) // if current denom is 25 then next denom to be used is 10
{
nextDenom = 10;
}
else if (denom == 10) // if current denom is 10 then next denom to be used is 5
{
nextDenom = 5;
}
else if (denom == 5) // if current denom is 5 then next denom to be used is 1
{
nextDenom = 1;
}
// try all possible number of coins of current denomination
int numberOfCoins = 0, ways = 0;
while ((numberOfCoins*denom) <= amount)
{
ways += countNumberOfWays(amount - (numberOfCoins*denom), nextDenom);
numberOfCoins += 1;
}
return ways;
}
public static void main(String[] args)
{
WaysOfMakingChange solution = new WaysOfMakingChange();
int amount = 20;
HashMap<AmountDenom, Integer> numberOfWays = new HashMap();
System.out.println("Number of ways of making change for 20 using denominations of 20,10,5 and 1 are:\n" +solution.countNumberOfWays(amount, 20, numberOfWays));
}
}
Order of the Algorithm
Time Complexity is O(nm)
Space Complexity is O(nm)
