Sorting Algorithm - Comb Sort
Given an array, sort the array using Comb Sort algorithm.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Comb sort is a comparison based sorting algorithm which improves on bubble sort.
In bubble sort, the adjacent elements are compared for sorting the array, so the gap between the elements that are compared is 1.
Comb sort uses a larger gap and works on bubble sort strategy. We define a variable gap and the elements separated by the gap are compared and swapped to get sorted order of elements. The gap is initialized as size of the array and after every iteration the gap is reduced by a shrink factor as described in the below algorithm steps. The iteration continues till the gap becomes 1. So the last iteration of this algorithm is same as a bubble sort iteration.
The best shrink factor has been found to be 1.3. This was found by the authors Stephen Lacey and Richard Box by testing Comb sort on over 200,000 random lists.
(Source: https://en.wikipedia.org/wiki/Comb_sort)
Algorithm:
1. Create variables gap and swapped and constant SHRINK_FACTOR and initialize as below:
i. gap = size of the array
ii. swapped = false
iii. SHRINK_FACTOR = 1.3
'swapped' is used to check whether any 2 elements have been swapped at the end of an iteration, like it is used in Bubble Sort algorithm for optimization.
2. Set swapped = false
3. Set gap = (int) (gap/SHRINK_FACTOR).
4. Iterate over the array from i = 0 to i < n - gap:
a. If array[i] > array[i + gap]
i. swap the elements array[i] and array[i + gap], to arrange in sorted order
ii. set swapped = true
5. Repeat steps 2-4 while gap != 1 and swapped = true
Examples:
1. Consider the array:
Initialization:
Size of array = 6
gap = 6, swapped = false
Iteration 1:
swapped = false
gap = gap/SHRINK_FACTOR = 6/1.3 = 4
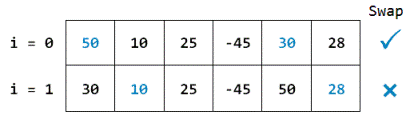
As i = 2, i + gap = 2 + 4 = 6, there is no element at index 6, so the iteration ends here.
Iteration 2:
swapped = false
gap = gap/SHRINK_FACTOR = 4/1.3 = 3
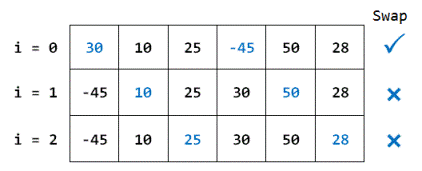
As i = 3, i + gap = 3 + 3 = 6, there is no element at index 6, so the iteration ends here.
Iteration 3:
swapped = false
gap = gap/SHRINK_FACTOR = 3/1.3 = 2
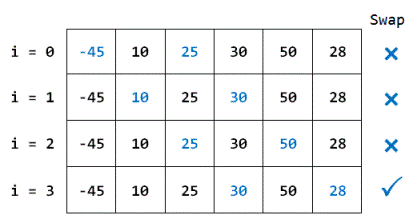
As i = 4, i + gap = 4 + 2 = 6, there is no element at index 6, so the iteration ends here.
Iteration 4:
swapped = false
gap = gap/SHRINK_FACTOR = 2/1.3 = 1
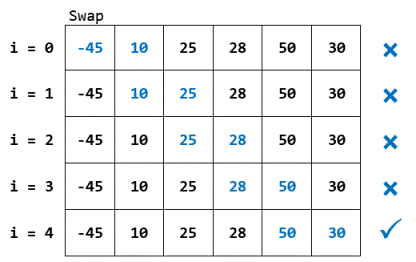
As i = 5, i + gap = 5 + 1 = 6, there is no element at index 6, so the iteration ends here.
As gap = 1, if we move on to next iteration, gap will become 1/1.3 = 0 so we will be comparing each element with itself. Hence the iterations end here and sorting is complete.
Hence the sorted array is:
2. When the array is already sorted:
Consider the sorted array: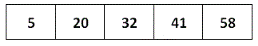
Initialization:
Size of array = 5
gap = 5, swapped = false
Iteration 1:
swapped = false
gap = gap/SHRINK_FACTOR = 5/1.3 = 3
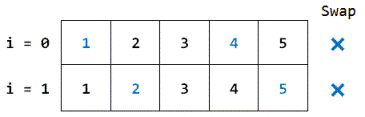
As i = 2 >= n - gap (5 - 3 = 2), iteration ends here.
As swapped is false now, no further iterations will take place and the loop ends here.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.sunny;
import java.util.Arrays;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given an array, sort the array using Comb Sort algorithm.
*
* @author Sunny
*/
public class CombSort {
private static final float SHRINK_FACTOR = 1.3f;
public static void combSort(int[] array) {
if(array == null || array.length < 2) {
return;
}
int n = array.length;
int gap = n;
boolean swapped = false;
do {
gap = (int) (gap / SHRINK_FACTOR);
for (int i = 0; i < n - gap; i++) {
if (array[i] > array[i + gap]) {
swap(array, i, i + gap);
swapped = true;
}
}
} while (gap > 1 && swapped);
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String args[]) {
int[] array = {50, 10, 25, -45, 30, 28};
combSort(array);
System.out.println(Arrays.toString(array));
}
}
Order of the Algorithm
Time Complexity is O(n^2) in the worst case. Best case time complexity is O(n) when the array is already sorted, in which case swapped is false and we exit the loop after first iteration.
Space Complexity is O(1) auxiliary space.
