Construct the binary tree from its parent array representation
Given parent array representation of a tree, construct the tree using this parent array. In this parent array representation, a node would be constructed with values taken from indices of this array. For element parent[i], a node would be constructed with value 'i'. And parent node for this constructed node with value 'i' would be node with value parent[i]. If parent[i] is -1, then we make the node with value 'i' as the root of the tree. For example, for the parent array {3, 5, 0, -1, 5, 3, 0} - parent[0] is 3 and also parent[5] is 3, therefore node with value 3 would be parent node for nodes with values 0 and 5. Similarly, parent[1]=parent[4]=5, therefore node with value 5 would be parent node for nodes with values 1 and 4. Then parent[2]=parent[6]=0 implies that node with value 0 would be parant node for nodes with values 2 and 6. Here, parent[3] is -1 therefore, node 3 would be the root node for this tree.
The complete constructed tree for parent array {3, 5, 0, -1, 5, 3, 0} would look like following: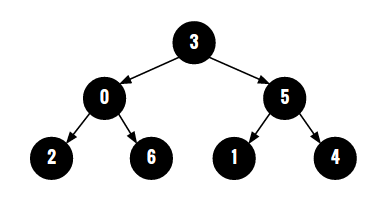
For parent array {-1, 0, 1, 5, 1, 0}, constructed binary tree would be :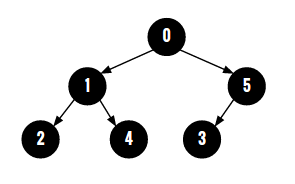
Video coming soon!
Subscribe for more updates
Algorithm/Insights
There are at least two approaches to solve this problem. We will be covering both the approaches here.
First Approach: (constructTreeTopDown(int[] parent) in the code snippet implements this)
This is a more intuitive approach and it constructs tree in top down manner starting from the root node.
First we search for element with value -1 in parent array. Let the index of that element be 'rootIndex'. We create a node with value 'rootIndex' and mark that node as the root for the tree. Now we make a call to function constructTreeTopDownRec(currentNode = root, index = rootIndex, parentArray = parent) which searches for elements with value rootIndex in parent array. If such elements are found, then it creates nodes out of the found indices, makes them children of the root and constructs sub-trees rooted at these created nodes(children) by making recursive calls. The base case of this recursive function constructTreeTopDownRec(currentNode, index, parent) occurs when it can't find elements with value 'index' in parent array. This implies that the currentNode is leaf node and therefore it does not have any sub-trees rooted at itself.
The time complexity for this approach is O(n^2) since for constructing 'n' nodes, parent array has to be scanned 'n' times.
Second approach: (constructTreeBottomUp(int[] parent) in the code snippet implements this)
This approach is a more of a bottom up approach and takes O(n) time. Let's see how:
1. Create a 'constructed' array of size same as that of parent array. constructed[i] stores the reference to the node with value i. Initialize all elements to null references.
2. Now to construct each node of this constructed array(the tree), call constructNode(i, constructed, parent) with 'i' taking every value from all indices of constructed array.
3. In the constructNode(i, constructed, parent) function -
3a. If constructed[i] is not null, then we know that a node is already constructed with value 'i', and therefore we return.
3b. If parent[i] is -1, then this implies that node with value 'i' is the root node for this tree and hence we return by constructing a new tree node with value 'i' and marking this newly created node as the root of the tree.
If both 3a and 3b conditions above are not true, then
3c. we first construct a parent node for this node(with value 'i') by making a recursive call constructNode(parent[i], constructed, parent).
3d. Once the parent node for node 'i' is constructed, we actually construct a new tree node with value 'i'. Notice that in the previous steps, we did not create node for this current index 'i'.
3e. Now we attach created node 'i' with its parent node. If the parent node's left child is not null, then we must attach this current node as the right child to its parent node otherwise we attach current node as the left child to its parent node.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution to construct binary tree from its parent array representation.
* @author Nilesh
*/
public class CreateTreeFromParentArray {
final static int INVALID_INDEX = -1;
private class TreeNode
{
int data;
TreeNode left;
TreeNode right;
TreeNode(int data)
{
this.data = data;
}
}
TreeNode root;
private void constructNode(int i, TreeNode[] constructed, int[] parent)
{
// node already created for this index 'i'
if (constructed[i] != null)
{
return;
}
// we need to create a root with value as this index 'i'
// there would be no parent node for root,
// hence we returning after creating root node
if (parent[i] == -1)
{
constructed[i] = new TreeNode(i);
root = constructed[i];
return;
}
// first we create a parent node, then create current node itself
// and finally attach current node to its parent
if (constructed[parent[i]] == null)
{
constructNode(parent[i], constructed, parent);
}
// create node reference using value as this index 'i'
constructed[i] = new TreeNode(i);
// attach node to its parent
if (constructed[parent[i]] != null) // sanity check
{
if (constructed[parent[i]].left == null)
{
constructed[parent[i]].left = constructed[i];
}
else
{
constructed[parent[i]].right = constructed[i];
}
}
}
public TreeNode constructTreeBottomUp(int[] parent)
{
TreeNode[] constructed = new TreeNode[parent.length];
for (int i = 0; i < constructed.length; i++)
{
constructNode(i, constructed, parent);
}
return root;
}
private void constructTreeTopDownRec(TreeNode currentNode, int currentNodeValue, int[] parent)
{
// search for currentNodeValue in parent array
// if two values found, we create two children for currentNode
// if only one value found, then we create only left child
// if no value found, then this currentNode is leaf node.
int indexFirstChild = -1, indexSecondChild = -1;
for (int i = 0; i < parent.length; i++)
{
if (currentNodeValue == parent[i])
{
if (indexFirstChild == -1)
{
indexFirstChild = i;
}
else
{
indexSecondChild = i;
break;
}
}
}
// no child found for this currentNode
if (indexFirstChild == -1)
{
return;
}
// create left child and left sub-tree rooted at left child
currentNode.left = new TreeNode(indexFirstChild);
constructTreeTopDownRec(currentNode.left, indexFirstChild, parent);
// if right child found then create node for it
// then create right sub-tree rooted at right child
if (indexSecondChild != -1)
{
currentNode.right = new TreeNode(indexSecondChild);
constructTreeTopDownRec(currentNode.right, indexSecondChild, parent);
}
}
public TreeNode constructTreeTopDown(int[] parent)
{
// search for value -1, create root out of it
// and call recursive sub-routine to create complete tree
int rootIndex = INVALID_INDEX;
for (int i = 0; i < parent.length; i++)
{
if (parent[i] == -1)
{
rootIndex = i;
break;
}
}
if (rootIndex != INVALID_INDEX)
{
this.root = new TreeNode(rootIndex);
}
constructTreeTopDownRec(root, rootIndex, parent);
return root;
}
public void printInorder(TreeNode root)
{
if (root == null) return;
printInorder(root.left);
System.out.print(root.data + ", ");
printInorder(root.right);
}
public static void main(String[] args)
{
CreateTreeFromParentArray solution = new CreateTreeFromParentArray();
int[] parent = {3, 5, 0, -1, 5, 3, 0};
TreeNode root = solution.constructTreeBottomUp(parent);
// TreeNode root = solution.constructTreeTopDown(parent);
/*
3
0 5
2 6 1 4
*/
System.out.println("Inorder traversal for constructed tree is: ");
solution.printInorder(root);
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
