Find minimum edit distance between given two strings
Minimum Edit distance between two strings str1 and str2 is defined as the minimum number of insert/delete/substitute operations required to transform str1 into str2. For example if str1 = "ab", str2 = "abc" then making an insert operation of character 'c' on str1 transforms str1 into str2. Therefore, edit distance between str1 and str2 is 1. You can also calculate edit distance as number of operations required to transform str2 into str1. For above example, if we perform a delete operation of character 'c' on str2, it is transformed into str1 resulting in same edit distance of 1.
Looking at another example, if str1 = "INTENTION" and str2 = "EXECUTION", then the minimum edit distance between str1 and str2 turns out to be 5 as shown below. All operations are performed on str1.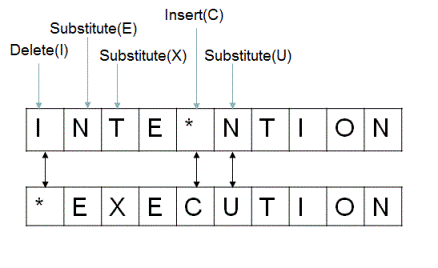
Credits for above example: Stanford University (https://web.stanford.edu/class/cs124)
Given two strings, write a program to find out the minimum edit distance between them.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
The problem is not that difficult as it might appear to be when we break it down into smaller sub-problems and try to solve them.
Let the first string str1 of length 'm' be "A1A2A3 ... Am" where 'A1', 'A2' denote the individual characters of str1. Let the second string str2 of length 'n' be "B1B2B3 ... Bn". To compute the edit distance between these two strings, let's start comparing last characters of str1 and str2. If character 'Am' is equal to character 'Bn', then we just need to compute edit distance between strings "A1A2A3 ... Am-1" and "B1B2B3 ... Bn-1". But if the character 'Am' is not equal to character 'Bn' then we have got following three choices to use -
1. Insert character 'Bn' at the end of the string str1. Modified str1 would then look like "A1A2A3 ... AmBn". After this operation, we can now start computing edit distance between string "A1A1A2 ... Am" and "B1B2B3 ... Bn-1" because we don't need to consider last character 'Bn' of str2 which matches with newly inserted last character 'Bn' in str1. Notice how after performing insert operation on str1, we need to consider first 'm' characters of str1 and first 'n-1' characters of str2 for computing edit distance.
2. Delete last character 'Am' of str1 and compute edit distance between strings "A1A2A3 ... Am-1" and "B1B2B3 ... Bn". Notice that after performing delete operation on str2, we need to consider first 'm-1' characters of str1 and first 'n' characters of str2 for computing edit distance.
3. Substitute last character 'Am' of str1 by character 'Bn'. Now the modified str1 looks like "A1A2A3 ... Am-1Bn" and str2 is still "B1B2B3 ... Bn". After this substitute operation, we now need to compute edit distance between strings "A1A2A3 ... Am-1" and "B1B2B3 ... Bn-1". Notice that after performing substitute operation on str1, we now need to consider first 'm-1' characters of str1 and first 'n-1' characters of str2 for computing edit distance.
How do we decide which one of these three choices to use? Well, we can't decide that in advance and we need to try out all three choices and use the result of the choice which gives us minimum edit distance.
If we want to express above steps in a function call 'findEditDistance(String str1, String str2, int m, int n)' then that function would look like following -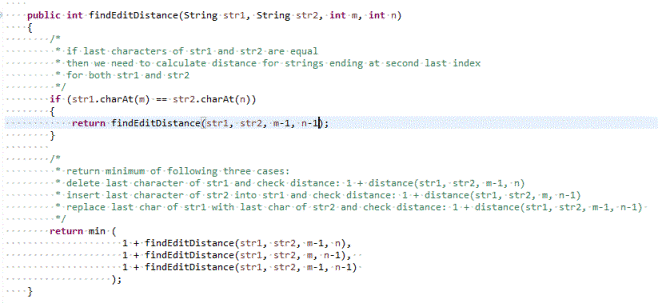
Now as you can observe, this function is recursive in nature and therefore we need to define base case for this recursion.
The base case would be -
1. If length of str1 is 0, then we need to insert all characters of str2 into str1 to make them equal. Therefore, edit distance between str1 and str2 when str1 is empty is length of str2.
2. If length of str2 is 0, then we need to delete all characters of str1 to make it equal to str2. Therefore, edit distance between str1 and str2 when str2 is empty is length of str1.
Please checkout function 'findDistance(String str1, String str2, int m, int n)' in code snippet for implementation details. The time complexity of above recursive algorithm is exponential since at every comparison step, we are making three choices making it roughly O(3^n) algorithm.
Dynamic Programming approach: Now let's see how we can optimize the time complexity of this algorithm. The partial recursion tree of call sequence for function findDistance(String str1, String str2, int m, int n) would look like following - 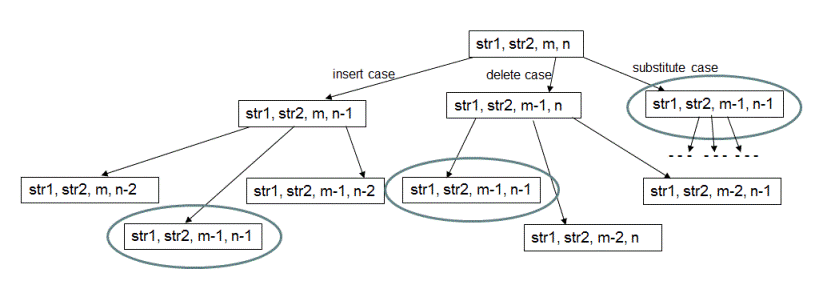
As highlighted above, there are function calls with same arguments which are being computed again and again. To avoid these redundant computations, we use dynamic programming based approach.
In this method, we use bottom up approach to compute the edit distance between str1 and str2. We start by computing edit distance for smaller sub-problems and use the results of these smaller sub-problems to compute results for sub-sequent larger problems. The results are stored in a two dimensional array as shown below.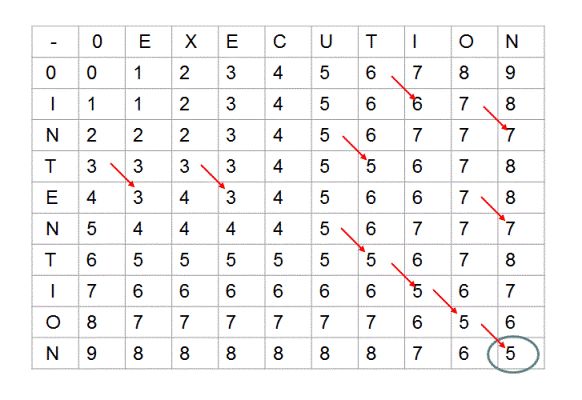
Each cell (m,n) of this array represents distance first 'm' characters of str1 and first 'n' characrers of str2. For example, when 'm' is 0, distance between str1 which is of 0 length and str2 of 'n' length is 'n'. Please observe 0th row of above matrix. Same is the case for values in 0th column where str2 is of 0 length.
Now in this matrix, for cell (m,n) which represents distance between str1 of length 'm' characters and str2 of length 'n' characters, if 'm'th character of str1 and 'n'th character of str2 are same, then we simply need to fill cell(m,n) using value of cell (m-1, n-1) which represents edit distance between first 'm-1' characters if str1 and first 'n-1' characters of str2. Notice the red arrows in the above array.
If 'm'th character of str1 is not equal to 'n'th character of str2, then we choose minimum value from following three cases-
1. Delete 'm'th character of str1 and compute edit distance between 'm-1' characters of str1 and 'n' characters of str2. For this computation, we simply have to do - (1 + array[m-1][n]) where 1 is the cost of delete operation and array[m-1][n] is edit distance between 'm-1' characters of str1 and 'n' characters of str2.
2. Similarly, for the second case of inserting last character of str2 into str1, we have to do - (1 + array[m][n-1]).
3. And for the third case of substituting last character of str1 by last character of str2 we use - (1 + array[m-1][n-1]).
Please checkout function 'findDistance(String str1, String str2)' in code snippet for implementation details. The time and space complexity of this method is O(mn) where 'm' is the length of str1 and 'n' is the length of str2.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Minimum edit distance between two strings using bottom-up dynamic programming algorithm in O(mn).
* @author Nilesh
*/
public class EditDistanceStrings
{
final static int ERROR_INPUT = -1;
private int min(int a, int b)
{
return (a<b)?a:b;
}
private int min(int a, int b, int c)
{
return min(min(a,b),c);
}
public int findDistance(String str1, String str2, int m, int n)
{
// if either of the strings is null, distance cannot be computed
if (str1 == null || str2 == null)
{
return ERROR_INPUT;
}
// if str1 is an empty string, then insert all 'n' characters of str2 into str1
if (m == 0)
{
return n;
}
// if str2 is an empty string, then remove all 'm' characters of str1
if (n == 0)
{
return m;
}
/*
* if last characters of str1 and str2 are equal
* then we need to calculate distance for strings ending at second last index
* for both str1 and str2
*/
if (str1.charAt(m-1) == str2.charAt(n-1))
{
return findDistance(str1, str2, m-1, n-1);
}
/*
* return minimum of following three cases:
* delete last character of str1 and check distance: 1 + distance(str1, str2, m-1, n)
* insert last character of str2 into str1 and check distance: 1 + distance(str1, str2, m, n-1)
* replace last char of str1 with last char of str2 and check distance: 1 + distance(str1, str2, m-1, n-1)
*/
return min (
1 + findDistance(str1, str2, m-1, n),
1 + findDistance(str1, str2, m, n-1),
1 + findDistance(str1, str2, m-1, n-1)
);
}
public int findDistance(String str1, String str2)
{
// if either of the strings is null, distance cannot be computed
if (str1 == null || str2 == null)
{
return ERROR_INPUT;
}
// all values are by default initialized to 0 by JVM
int[][] distanceTable = new int[str1.length()+1][str2.length()+1];
int numRows = str1.length() + 1;
int numCols = str2.length() + 1;
for (int m = 0; m < numRows; m++)
{
for (int n = 0; n < numCols; n++)
{
// if length of str1 is 0, we have no option but to insert all of str2
if (m == 0)
{
distanceTable[m][n] = n;
}
// if length of str2 is 0, delete all of str1 to make it match with str2
else if (n == 0)
{
distanceTable[m][n] = m;
}
/*
* if last characters of str1 and str2 are equal, compute distance ending at
* second last characters for both str1 and str2
*/
else if (str1.charAt(m-1) == str2.charAt(n-1))
{
distanceTable[m][n] = distanceTable[m-1][n-1];
}
/*
* else use minimum of following three cases:
* delete last character of str1 and check distance: distance(str1, str2, m-1, n)
* insert last character of str2 into str1 and check distance: distance(str1, str2, m, n-1)
* replace last char of str1 with last char of str2 and check distance: distance(str1, str2, m-1, n-1)
*/
else
{
distanceTable[m][n] = min (
1 + distanceTable[m-1][n],
1 + distanceTable[m][n-1],
1 + distanceTable[m-1][n-1]
);
}
}
}
return distanceTable[numRows-1][numCols-1];
}
public static void main(String[] args)
{
EditDistanceStrings solution = new EditDistanceStrings();
System.out.print("minimum edit distance between \"intention\" and \"execution\" is: \n");
System.out.println(solution.findDistance("intention", "execution"));
}
}
Order of the Algorithm
Time Complexity is O(mn)
Space Complexity is O(mn)
