Find the Element That Appears Once in an Array
Find the element that occurs only once in a given set of integers while all the other numbers occur thrice.
Example -
Input : 3 3 3 4
Output: 4
Input : 5 5 4 8 4 5 8 9 4 8
Output: 9
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
The idea is to count the set bits in all the given numbers. As we know, all the elements(except one) occur 3 times so their respective set bits will also occur 3 times. Thus when we take modulus 3 of the sum of all set bits we will be left with only the bits of that number which occurs once.
The steps of the algorithm are as following:
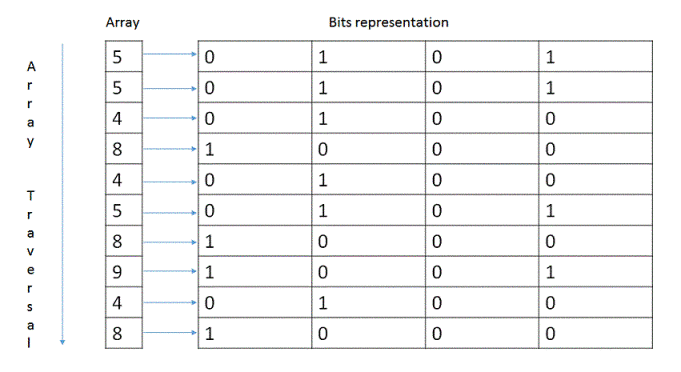
1: Create countSetBits[] array of size 32(for representing 32 bit integer) where,
countSetBits[i] represents count of ith set bit of all elements in the input array.
Initially all elements of countSetBits[] array are 0.
2. Traverse all the elements of the input array to populate countSetBits, by doing step #3 for each of them.
3. Take the element and check for its set bits. If the ith bit is found to be set, then in the countSetBits[] array increment the count of the element at the index 'i'.
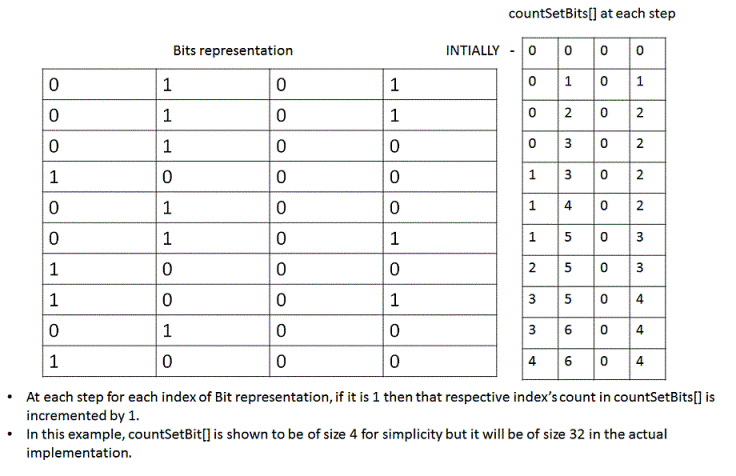
4. After finishing the above operation for all the elements of the input array, the elements of countSetBits[] would represent count of all set bits in the elements of input array. Perform the modulus 3 operation on each element of the countSetBits[] array. Taking mod with 3 will determine the number of times that respective index was set in all the elements of given input array. If we get a remainder 1 at an index 'j', then that means in the number that occurs only once, we have a set bit of index 'j'. We will get a remainder 2 only if the given question is violated with two instances of a number.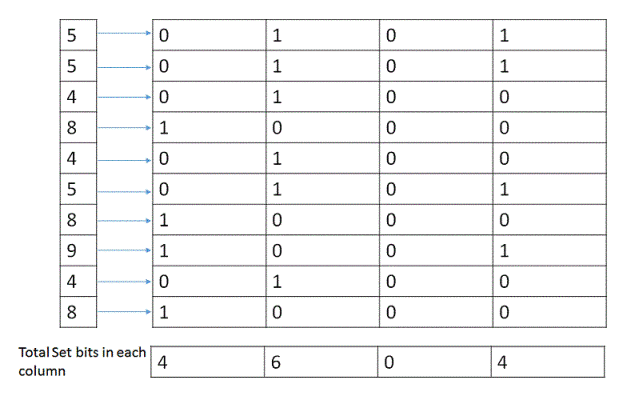
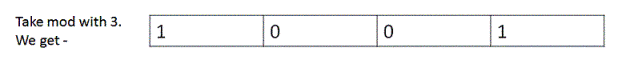
5. Finally after modulus of each element in countSetBits[], simply transform the binary representation into decimal.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.abhishek;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution for finding out the number that occurs once.
*
* @author Abhishek
*/
public class BitWiseMod {
/**
* Method to find the element that occurs only once in the input array
* while all the other numbers occur N times.
*
* @param arr is input array.
* @param N is number of times all elements, except one, are occurring in the input array.
* @return the number which occurs only once in the input array.
*/
public int findRequiredNum(int arr[], int N) {
// For counting set bits in all given numbers.
int countSetBit[] = new int[32];
// For each element run the loop.
for (int i = 0; i < arr.length; i++) {
// Find the set bits in the current element.
for (int k = 0; k < 32; k++) {
int kthSetBit = 1 << k;
// If the kth bit is set, then increment the count of countSetBit[k].
if ((arr[i] & kthSetBit) == kthSetBit)
countSetBit[k]++;
}
}
// Required number.
int occurredOnce = 0;
// Iterate over countSetBit.
for (int i = 0; i < 32; i++) {
/*
* Find the remainder of each element with N so as to see what is
* the representation of the single occurred element.
*/
countSetBit[i] = countSetBit[i] % N;
/*
* After mod operation, each element of countSetBit represent bits
* of required element(occurredOnce). Therefore, set ith bit in
* occurredOnce if countSetBit[i] is 1.
*/
if (countSetBit[i] == 1)
occurredOnce = occurredOnce | (1 << i);
}
return occurredOnce;
}
/**
* Method for testing the algorithm.
*
* @param args
*/
public static void main(String args[]) {
int[] arr = { 5, 5, 4, 8, 4, 5, 8, 9, 4, 8 };
System.out.print("Input Matrix : ");
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
BitWiseMod solution = new BitWiseMod();
/*
* Since all elements in the input array, except one, occur 3 times,
* pass 3 as argument in call to findRequiredNum.
*/
System.out.println("\n\nThe number which occured only once is: " + solution.findRequiredNum(arr, 3));
}
}
Order of the Algorithm
Time Complexity is O(32.n) = O(n)
Space Complexity is O(1) As constant size array is required.
