Find the 'n'th most frequent number in array
Given an array of numbers and a positive integer 'n', find 'n'th most frequent occurring number in that array. If there are more than one numbers which are occurring 'n'th most frequently, then you can return any one of such integers.
Example: For the input array {1,2,2,2,4,4,4,4,5,5,5,5,5,7,7,8,8,8,8}
if n = 1, then the output returned should be 5 because it is the most frequent number,
if n = 2, output can be either 4 or 8 since any of these numbers could be considered as the 2nd most frequent number,
if n = 3, again output can be either 4 or 8
if n = 4, output should be 2.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Simple Idea: One of the simple ideas that could be used is to create a frequency table which stores the frequency of occurrence for each element in the array. Then if we sort this table according to the frequencies, we can easily tell the number which is 'n'th most frequent. If there are 'm' elements in the given array(m > n), frequency table could be created in O(m) time using hash-table and then sorting this table and picking 'n'th most frequent number would take O(mlog(m)) time.
Optimized Approach: We can further reduce the time complexity to O(nlog(m)) by making use of max-heap('m' is the length of the input array). This approach would be very similar to heap sort algorithm. For understanding the concept of max-heap and heap sort you can refer this post.
This approach uses following steps -
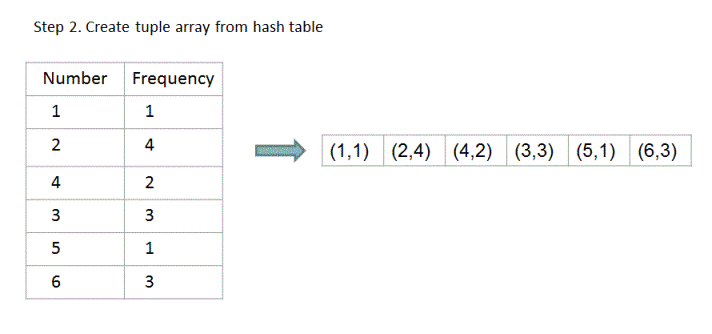
1. Using hash table, we first create a frequency table which stores the frequency of occurrence for each number. In this hash table, we define (key, value) tuple as tuple (number 'i', frequency of 'i').
2. Now we traverse this hash table and create an array which stores these (number, frequency) tuples.
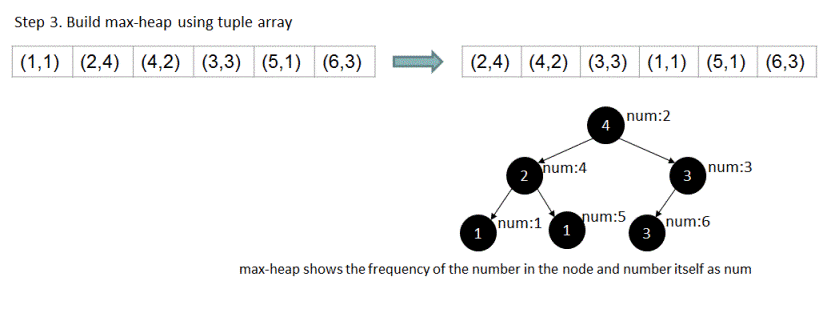
3. We build the max-heap using this tuple array created in step #2.
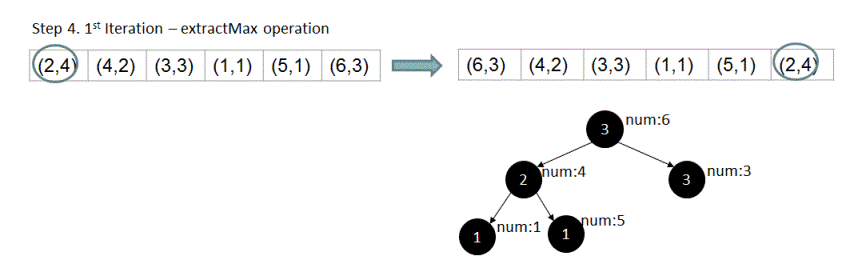
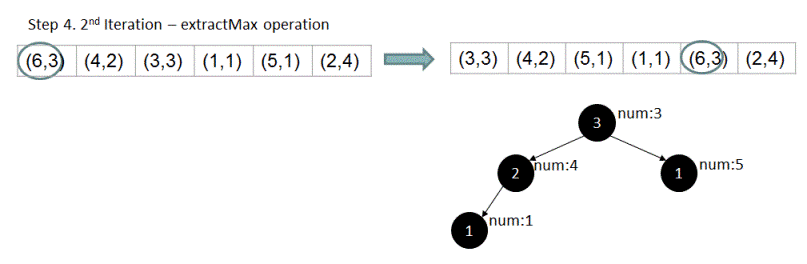
4. By property of max-heap, the root element(or element at 0th index) would be the most frequent element and hence would be the output for input n = 1. For finding out 2nd most frequent element, we swap the root element with the last element and re-arrange the remaining 'm - 1' elements to form a max-heap(let the length of the array be 'm'). Now in this newly created heap(without using the previous root), new root element would again be the largest element in the 'm - 1' elements and hence it would be the 2nd largest element in all 'm' elements.
5. It follows that if we repeat step #4 'n' times, we should be able to find out 'n'th most frequent number.
If 'm' is the length of the input array then step #1, #2 and #3 take O(m) time. Step #4 takes O(log(m)) time which is executed 'n' number of times hence overall time complexity of this algorithm is O(nlog(m)). Space complexity of this algorithm is O(m).
For array {1,2,2,2,2,4,4,3,3,3,5,6,6,6}, if n = 4, output should be 4 . Let's see how exactly the above algorithm works for this input.
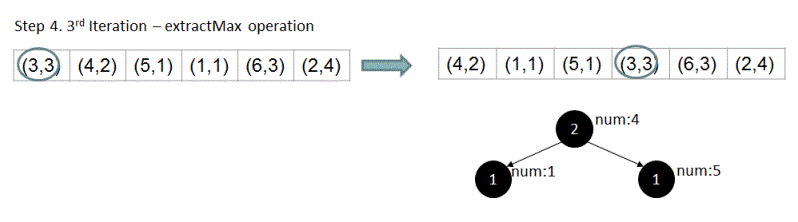
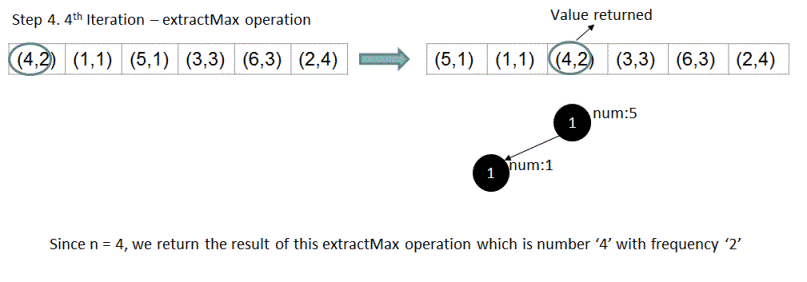
Please feel free to add comments below in case of any queries/feedback.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Finds 'n'th most frequent number from the given array in nlog(m) time.
* @author Nilesh
*/
import java.util.HashMap;
import java.util.Map;
public class NthMostFrequentNumber
{
private class NumberFrequencyTuple
{
int number;
int frequency;
public NumberFrequencyTuple(int number, int frequency)
{
this.number = number;
this.frequency = frequency;
}
}
private void swap(NumberFrequencyTuple[] array, int i, int j)
{
NumberFrequencyTuple tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
private void maxHeapify(NumberFrequencyTuple[] array, int curIndex, int heapSize)
{
// left child in heap
int leftChild = 2*curIndex+1;
// right child in heap
int rightChild = 2*curIndex+2;
// index pointing to the largest element(out of node and its two children)
int largestIndex = curIndex;
if(leftChild < heapSize && (array[leftChild].frequency > array[curIndex].frequency))
{
largestIndex = leftChild;
}
if(rightChild < heapSize && (array[rightChild].frequency > array[largestIndex].frequency))
{
largestIndex = rightChild;
}
// make the largest element as node and maxHeapify the corresponding sub-tree
// since the swap operation could result in violation of max-heap property for corresponding sub-tree
if(largestIndex != curIndex)
{
swap(array, curIndex, largestIndex);
maxHeapify(array, largestIndex, heapSize);
}
}
private void buildMaxHeap(NumberFrequencyTuple[] array, int heapSize)
{
// find index of the last internal node
int lastElementIndex = array.length - 1;
int lastInternalNodeIndex = (lastElementIndex - 1)/2;
// call maxHeapify for all internal nodes
for(int i = lastInternalNodeIndex; i >= 0; i--)
{
maxHeapify(array, i, heapSize);
}
}
private int extractMax(NumberFrequencyTuple[] array, int heapSize)
{
int maxElement = array[0].number;
swap(array, 0, heapSize-1);
maxHeapify(array,0, heapSize-1);
return maxElement;
}
public int findNthMostFrequentNumber(int[] array, int n)
{
if (array == null || array.length < 1 || array.length < n)
{
System.out.println("Invalid input case");
return -1;
}
// build hashTable containing frequency of each element in the array
HashMap<Integer, Integer> frequencyTable = new HashMap<Integer, Integer>();
for (int i = 0; i < array.length; i++)
{
if (frequencyTable.get(array[i]) == null)
{
frequencyTable.put(array[i], 1);
}
else
{
int prevFrequency = frequencyTable.get(array[i]);
frequencyTable.put(array[i], prevFrequency + 1);
}
}
// check if the number of frequencies we have got is at least equal to 'n'
if (frequencyTable.size() < n)
{
System.out.println("nth most frequent number cannot be found for this input array");
return -1;
}
// then create the array of tuples(number, frequency) out of hashTable of frequencies
NumberFrequencyTuple[] list = new NumberFrequencyTuple[frequencyTable.size()];
int i = 0;
for (Map.Entry<Integer, Integer> entry : frequencyTable.entrySet())
{
list[i] = new NumberFrequencyTuple(entry.getKey(), entry.getValue());
i += 1;
}
// build max-heap using this array of tuples
int heapSize = list.length;
buildMaxHeap(list, heapSize);
// do extractMax operation 'n' times on this max-heap.
// return the result of last extractMax operation
int result = -1;
for (i = 0; i < n; i++)
{
if (i == n-1)
{
result = extractMax(list, heapSize);
}
else
{
extractMax(list, heapSize);
}
heapSize -= 1;
}
return result;
}
public static void main(String[] args)
{
NthMostFrequentNumber solution = new NthMostFrequentNumber();
int[] array = {1,2,2,2,2,3,3,4,4,4,5,6,6,6};
int n = 3;
System.out.println("Nth most frequent number is:\n" + solution.findNthMostFrequentNumber(array, 4));
}
}
Order of the Algorithm
Time Complexity is O(nlog(m)) m: input array length, n: 'n'th most frequent number
Space Complexity is O(m)
