Generate all subsets of a given set
Given a set, generate all possible subsets of it. For example if the input set is {1,2,3} then the program should return the set containing all possible subsets of it. Expected output - {{},{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The idea to generate all possible subsets is simple.
1. Start by adding an empty set to all possible subsets.
2. For each set - 'Set_i' in all possible subsets, create a new set - 'Set_i_new' by adding an element from given set to 'Set_i'. Add this newly generated 'Set_i_new' to all possible subsets.
3. Repeat step #2 for all elements in given set. This step is done using recursion.
For example, if the input is the set {1,2,3} then to generate all possible subsets we start by adding an empty set - {} to all possible subsets. Now we add element 1 to this empty set to create set {1} and we add this set {1} to all possible subsets. All possible subsets at this point has set {} and set {1} in it. Now we add element 2 to all sets in all possible subsets to create new sets {2}, {1,2}. We add these newly created sets to all possible subsets. We continue this process till all elements from given set are considered for generating all possible subsets.
Please checkout function findAllSubsets(ArrayList
Recursion tree generated using above algorithm is shown below.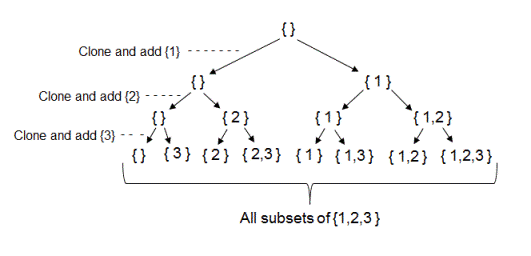
The time complexity of this algorithm is (2^n) as can be easily observed from the above recursion tree. The extra space used is of order O(1). Note that the space taken to store all possible subsets is not counted as extra space since it is anyway required to store the result.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Starts from an empty set to generate all possible subsets of given set using recursion
* @author Nilesh
*/
public class AllSubsets
{
private ArrayList<Integer> cloneSet(ArrayList<Integer> input)
{
ArrayList<Integer> clone = new ArrayList();
for (int i = 0; i < input.size(); i++)
{
clone.add(input.get(i));
}
return clone;
}
public void findAllSubsets(ArrayList<ArrayList<Integer>> allSubsets, ArrayList<Integer>set, int currIndex)
{
// base case: if all elements of given set are considered for all possible subsets
if (currIndex == set.size())
{
return;
}
// need to get the size in advance
// since adding new sets to allSubsets will increase its size dynamically.
int allSubSetsSize = allSubsets.size();
ArrayList<Integer> newSet;
// for each set - allSubsets[i] in allSubsets:
// 1. create new set by adding element placed at 'currIndex' in the given set
// 2. add this newly created set to 'allSubsets'
for (int i = 0; i < allSubSetsSize; i++)
{
newSet = cloneSet(allSubsets.get(i));
newSet.add(set.get(currIndex));
allSubsets.add(newSet);
}
// include next element from given set in allSubsets
findAllSubsets(allSubsets, set, currIndex+1);
}
public ArrayList<ArrayList<Integer>> findAllSubsets(ArrayList<Integer> set)
{
ArrayList<ArrayList<Integer>> allSubsets = new ArrayList();
// add empty set to all possible subsets
allSubsets.add(new ArrayList<Integer>());
// use empty set to generate all possible subsets of given set using recursion
findAllSubsets(allSubsets, set, 0);
return allSubsets;
}
public static void main(String[] args)
{
AllSubsets solution = new AllSubsets();
ArrayList<Integer> set = new ArrayList();
set.add(1);
set.add(2);
set.add(3);
ArrayList<ArrayList<Integer>> allSubsets = solution.findAllSubsets(set);
// only 2^n-1 subsets would be printed. Empty subset is not printed.
for (int i = 0; i < allSubsets.size(); i++)
{
ArrayList<Integer> tempSet = allSubsets.get(i);
for (int j = 0; j < tempSet.size(); j++)
{
System.out.print(tempSet.get(j) + ", ");
}
System.out.print("\n");
}
}
}
Order of the Algorithm
Time Complexity is O(2^n)
Space Complexity is O(1)
