Finding the power of a number in log(n) time | Recursion

Algorithm/Insights

The algorithm is simple implementation of following recurrence relation used to calculate 'a' to the power 'b' where 'a' and 'b' are integers.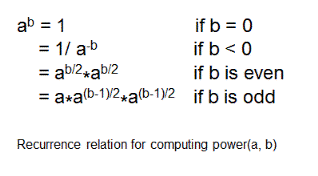

The generated recursion tree when above recurrence relation is implemented to calculate power(2,5) is shown below.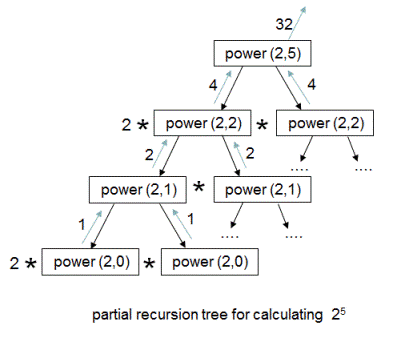

As you can observe, power(2,2,), power(2,1) are being computed multiple times. To avoid these redundant computations, we store the result in a temporary variable while making the recursive call and use this variable value sub-sequently. Please check 'public double power(int a, int b)' function in code snippet for implementation details.

The time complexity of this algorithm is O(log(b)) while computing power(a,b). This is because at every level in recursion sub-tree, we are doing only one computation(and using that value sub-sequently) and there are log(b) levels overall.

Please add comments below in case you have any feedback/queries.

Code Snippet

			
package com.ideserve.questions.nilesh;


/**
 * <b>IDeserve <br>
 * <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
 * Computes power of a number(power(a,b)) in log(b) time using recursion. 
 * @author Nilesh
 */

public class PowerOfNumber 
{
    // computes value of 'a' power 'b'
    public double power(int a, int b)
    {
        // base case
        if (b == 0)
        {
            return 1;
        }
        
        // a^(-b) = 1/(a^b)
        if (b < 0)
        {
            return 1/power(a,-b);
        }
        
        if (b%2 == 0) // if 'b' is even
        {
            return power(a, b/2)*power(a, b/2);
        }
        else // if 'b' is odd
        {
            return a*power(a, (b-1)/2)*power(a, (b-1)/2);
        }
    }
    
    public static void main(String[] args) 
    {
        PowerOfNumber solution = new PowerOfNumber();
        
        int a = -2, b = -3;
        
        System.out.println(solution.power(a, b));
    }
}
		

Order of the Algorithm

Time Complexity is O(log(b)) while computing power(a,b)
Space Complexity is O(1)