Implement a fair coin from a given unfair coin
Given an unfair coin, where probability of HEADS coming up is P and TAILS is (1-P), implement a fair coin from the given unfair coin.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
We need to create a system which returns HEADS and TAILS with equal probability.
Let us define an event = flipping the unfair coin twice.
Let us observe probability of all possible events.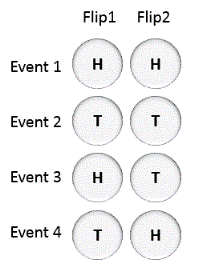
Event 1: Probability of HEADS coming up in both is P*P = P2
Event 2: Probability of TAILS coming up in both is (1-P)*(1-P) = (1-P)2
Event 3: Probability of HEADS coming up in first and TAILS in second is P*(1-P)
Event 4: Probability of TAILS coming up in first and HEADS in second is (1-P)*P
If you observe carefully, you would notice that events #3 and #4 occur with equal probability of P*(1-P).
So, if we ignore events #1 and #2 of getting both HEADS or TAILS, since they have different probabilities, we are left with events #3 and #4 which occur with equal probability.
Now let us design a System where we keep generating events until we get 3rd or 4th event, and then return value which comes up in the first flip of that event. In another words, keep flipping the unfair coin two at a time, until they come up with different values, then return value of first flip of the coin (out of the two flips). Here is a code snippet for this system.
Let us now prove that the probability of getting HEADS or TAILS is same in this system.
Probability of getting HEADS in this system = Probability of getting HEADS in the first flip given that two flips resulted in different values.
Probability of getting TAILS in this system = Probability of getting TAILS in the first flip given that two flips resulted in different values.
As these are conditional probabilities, we apply Bayes' Theorem.
According to Bayes' Theorem, for 2 events A and B: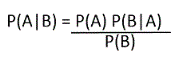
Now, Probability of getting HEADS in this system = Probability of getting HEADS in the first flip given that two flips resulted in different values.
Here,
A = Getting HEADS in the first flip
B = Getting different values in the 2 flips
We need to find the probabilities P(A), P(B) and P(B|A).
P(A) = Probability of getting head on flipping a coin = p
P(B) = Probability of getting HEADS in first flip and TAILS in second flip
OR
getting TAILS in first flip and HEADS in second flip
= Probability of Event 3 + Probability of Event 4
= p*(1-p) + (1-p)*p = 2p(1-p)
P(B|A) = Probability of getting different values in both flips given that first flip is HEADS
= Probability that second coin is TAILS
= (1-p)
Hence, Probability of getting HEADS in this system
= Probability of getting HEADS in the first flip given that two flips resulted in different values
= P(A|B)
= ( P*(1-P) ) / ( 2P(1-P) )
= 1/2
Similarly, Probability of getting TAILS in this system = 1/2
