Find index of 0 to replace to get longest continuous sequence of 1s
Given a binary array, find the index of 0 such that when that 0 is replaced with 1 results in longest continuous sequence of 1's. For example, for array {0,1,1,1,0,1,0} replacing 0 at 0th index with 1 results in a sequence of 1's with length 4 and replacing 0 at index 4 with 1 results in a sequence of 1's with length 5. Hence for this input array, output returned should be 4.
For array {0,0,1,1,1,1,0,0,1,1,1,1,0,1,1,0,1,0,1,1,1,1,0} longest sequence of 1's is obtained when we replace 0 at index 12 with 1.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The simple idea to solve this problem is to find out number of 1's on the both side of each 0. The 0 which has highest number of 1's around it is the 0 we are looking for. For example for array {0,0,1,1,1,1,0,0,1,1,1,1,0,1,1,0,1,0,1,1,1,1,0}
number of 1's around 0 with index 0 - 0
number of 1's around 0 with index 1 - 4
number of 1's around 0 with index 6 - 4
number of 1's around 0 with index 7 - 4
number of 1's around 0 with index 12 - 6
number of 1's around 0 with index 15 - 3
number of 1's around 0 with index 17 - 5
number of 1's around 0 with index 22 - 4
As you can see, if we replace 0 at index 12 with 1 we get sequence of 1's with length as 7 which would be the longest sequence we could get using this array.
Now to get number of 1's around 0, we can simply count them once we visit a 0 while traversing the complete array. This approach would take O(n^2) time.
Another approach to find 1's around each index of 0 uses following technique. 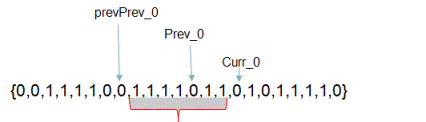
If the current index points to 0(say curr_0) and if we know the index which points to previous occurrence of 0(say prev_0) and if we also know the index which points to previous to previous occurrence of 0(say prevPrev_0) then subtracting (prevPrev_0 + 1) from curr_0 gives us the number of 1's that could be obtained by replacing 0 with 1 at index prev_0. This is because between indices prevPrev_0 and curr_0 there are all 1's except a single 0 at prev_0. Please observe above diagram carefully to get complete clarity.
In the function getRequiredIndex() in code snippet, we use same idea to find out the required index of 0. We traverse the complete array and if the current index 'i' points to 0 then we find out the length of longest sequence of 1's that could be obtained by replacing 0 at prev_0 by calculating: 'i' - (prevPrev_0 + 1). If this length is greater than maximum such length seen so far then we update maximum length seen so far to new calculated length.
This algorithm runs in O(n) time and with o(1) extra space.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Finds the index of 0 such that when that 0 is replaced with 1 results in longest continuous sequence of 1's.
* Runs in O(n) time.
* @author Nilesh
*/
public class ReplaceZeroToGetOnes
{
public int getRequiredIndex(int[] binaryArray)
{
int prevZeroIndex = -1, prevPrevZeroIndex = -1;
int maxLength = -1, requiredIndex = -1, currLength = -1;
for (int i = 0; i < binaryArray.length; i++)
{
if (binaryArray[i] == 0)
{
if (prevPrevZeroIndex != -1)
{
currLength = i - prevPrevZeroIndex - 1;
if (currLength > maxLength)
{
maxLength = currLength;
requiredIndex = prevZeroIndex;
}
}
prevPrevZeroIndex = prevZeroIndex;
prevZeroIndex = i;
}
}
// if number of 0s is less than 3
if (maxLength == -1)
{
if (prevPrevZeroIndex != -1) // if there are two 0s
{
// the length of 1s sequence after replacing 0 at 'prevPrevZeroIndex' would be 'prevZeroIndex'
// and the length of 1s sequence after replacing 0 at 'prevZeroIndex' would be (binaryArray.length - prevPrevZeroIndex - 1)
if (prevZeroIndex > (binaryArray.length - prevPrevZeroIndex - 1))
{
requiredIndex = prevPrevZeroIndex;
}
else
{
requiredIndex = prevZeroIndex;
}
}
else // if there is one or no 0s present
{
requiredIndex = prevZeroIndex;
}
}
return requiredIndex;
}
public static void main(String[] args)
{
ReplaceZeroToGetOnes solution = new ReplaceZeroToGetOnes();
int [] binaryArray = {0,0,1,1,1,1,0,0,1,1,1,1,0,1,1,0,1,0,1,1,1,1,0};
System.out.println(solution.getRequiredIndex(binaryArray));
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
