Merge Sort
Given an integer array, sort the array using Merge Sort algorithm.
Example:
Array: 12, 35, 87, 26, 9, 28, 7
Output: 7, 9, 12, 26, 28, 35, 87
Question Asked in
Goldman Sachs
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Merge sort is a comparison based algorithm that uses divide and conquer approach to sort an array in O(n logn) time.
Merge sort is a stable sort i.e. it preserves the order of same array elements after sorting.
Algorithm for Merge sort is:
Step 1. Divide the array into 2 halves recursively.
Step 2. Merge the divided parts in sorted order.
Here is an example that explains the algorithm: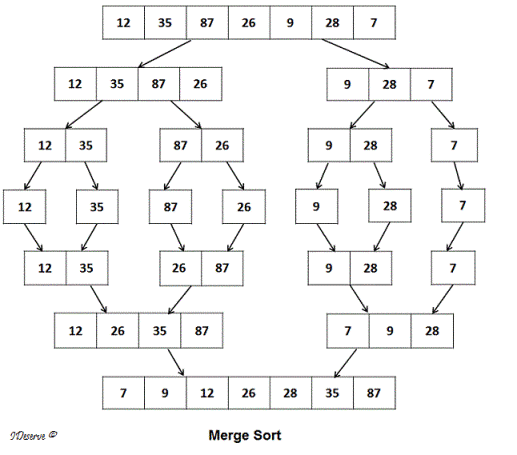
First, the array {12, 35, 87, 26, 9, 28, 7} is divided to sub arrays {12, 35, 87, 26} and {9, 28, 7} as shown in the image above.
Then {12, 35, 87, 26} is divided into {12, 35} and {87, 26}.
Next {12, 35} is divided into {12} and {35}
At this step, no further division is possible on single element arrays {12} and {35}.
Next step is to merge these arrays in sorted order to get {12, 35}
Next {87, 26} is divided into {87} and {26}
Similar as above, we merge these single element arrays in sorted order to get {26, 87}
Now we are at the step where we have {12, 35} and {26, 87}. We merge these subarrays in sorted order to form sorted array: {12, 26, 35, 87}
Similarly, {9, 28, 7} is also first divided recursively and then merged in sorted order to get sorted array {7, 9, 28}
Finally, we merge sorted subarrays {12, 26, 35, 87} and {7, 9, 28} in sorted order to get the sorted array {7, 9, 12, 26, 28, 35, 87}.
Here is the algorithm for merging 2 sorted arrays used by merge sort algorithm given in the code snippet section:
1. Create temporary arrays temp1 and temp2.
2. Copy elements of first subarray to temp1. So, temp1 = {12, 26, 35, 87}
3. Copy elements of second subarray to temp2. So, temp2 = {7, 9, 28}
4. Now copy elements from temp1 and temp2 to the original array in sorted order:
a. Traverse arrays temp1 and temp2 together:
b. If temp1[i] <= temp2[j], then copy temp1[i] to the original array and move i to next element in temp1.
c. Else copy temp2[j] to the original array and move j to next element in temp2.
d. If end of one temporary array is reached, then copy the elements of the other temporary array to the original array in the same order.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
import java.util.Arrays;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given an array, sort the array using Merge Sort algorithm.
*
* @author Saurabh
*/
public class MergeSort {
public static void mergeSort(int[] array) {
mergeSort(array, 0, array.length-1);
}
private static void mergeSort(int[] array, int start, int end) {
if(start < end) {
int mid = (start+end)/2;
mergeSort(array, start, mid);
mergeSort(array, mid+1, end);
merge(array, start, mid, end);
}
}
private static void merge(int[] array, int start, int mid, int end) {
int n1 = mid - start + 1;
int n2 = end - mid;
int[] temp1 = new int[n1];
int[] temp2 = new int[n2];
for(int i = 0; i < n1; i++) {
temp1[i] = array[start+i];
}
for(int j = 0; j < n2; j++) {
temp2[j] = array[mid+j+1];
}
int i = 0, j = 0, k = start;
while(i < n1 && j < n2) {
if(temp1[i] <= temp2[j]) {
array[k] = temp1[i];
i++;
} else {
array[k] = temp2[j];
j++;
}
k++;
}
while(i < n1) {
array[k] = temp1[i];
i++;
k++;
}
while(j < n2) {
array[k] = temp2[j];
j++;
k++;
}
}
public static void main(String[] args) {
int[] array = {12, 35, 87, 26, 9, 28, 7};
mergeSort(array);
System.out.println(Arrays.toString(array));
}
}
Order of the Algorithm
Time Complexity is O(n log n) in worst, best and average cases.
Space Complexity is O(n)
