Find minimum cost path in a matrix
Given a cost matrix having a cost at each cell. Find the minimum cost it will take to reach cell (m, n) from top left corner cell (0, 0) if the only allowed directions to move from a cell are right, down and diagonally down.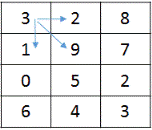
In this matrix, the minimum cost path to reach cell 3,2 is as shown: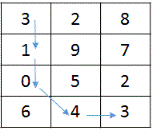
Hence, minimum cost is = 11
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Consider costMatrix as the given matrix and a position m,n
Minimum cost to reach m,n from 0,0 will be equal to the cost of cell m,n + total cost to reach cell m,n.
To reach cell m,n only permissible cells are the cells on left, up and diagonally up. (Because starting from 0,0 we can move further only to right, down and diagonally down cells. So, cells on left, up and diagonally up are the only cells from which we can reach to a cell.)
Recursive solution:
1. If m == 0 && n == 0, the costMatrix[0][0] is the solution.
2. Recursively find minimum cost for cells on left, up and diagonally up direction and add the minimum of these three to current cell cost.
Hence we have these conditions:
minimumCostPath(costMatrix, m, n) = costMatrix[m][n], if m == 0 && n == 0
minimumCostPath(costMatrix, m, n) = costMatrix[m][n] +
minimum(minimumCostPath(costMatrix, m - 1, n - 1),
minimumCostPath(costMatrix, m - 1, n),
minimumCostPath(costMatrix, m, n - 1));
Time complexity of the recursive algorithm is exponential.
Dynamic Programming solution:
The approach followed in recursive solution can be used to efficiently solve this problem by applying dynamic programming.
Create a minimumCostPath table of size m,n and define:
minimumCostPath[i][j] = minimum cost to reach (i, j) from (0, 0)
Clearly,
minimumCostPath[0][0] = costMatrix[0][0]
minimumCostPath[i][0] = minimumCostPath[i - 1][0] + costMatrix[i][0], for all values of i > 0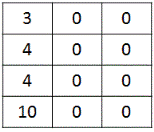
minimumCostPath[0][j] = minimumCostPath[0][j - 1] + costMatrix[0][j], for all values of j > 0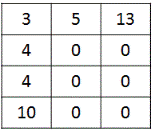
Next, we fill the minimumCostPath matrix by applying the same formula we used in recursive solution. Since, all the previous values will already have been calculated in the minimumCostPath matrix, we will not have to recalculate these as we did in the recursive solution.
minimumCostPath[i][j] = costMatrix[i][j] +
minimum(minimumCostPath[i - 1][j - 1],
minimumCostPath[i - 1][j],
minimumCostPath[i][j - 1])
Here, for calculating minimumCostPath[i][j] we use minimumCostPath[i - 1][j - 1], minimumCostPath[i - 1][j] and minimumCostPath[i][j - 1] because these are the only permissible cells from which we can reach minimumCostPath[i][j].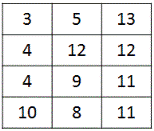
Finally, we return minimumCostPath[m][n].
Time complexity of DP algorithm is O(mn).
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given a cost matrix having a cost at each cell. Find the minimum cost it
* will take to reach cell (m, n) from top left corner cell (0, 0) if the only
* allowed directions to move from a cell are right, down and diagonally down.
*
* @author Saurabh
*/
public class MinimumCostPath {
public static int minimumCostPathRec(int[][] costMatrix, int m, int n) {
if (m < 0 || n < 0)
return Integer.MAX_VALUE;
if (m == 0 && n == 0)
return costMatrix[0][0];
return costMatrix[m][n]
+ minimum(minimumCostPathRec(costMatrix, m - 1, n - 1),
minimumCostPathRec(costMatrix, m - 1, n),
minimumCostPathRec(costMatrix, m, n - 1));
}
public static int minimumCostPathDP(int[][] costMatrix, int m, int n) {
int[][] minimumCostPath = new int[m+1][n+1];
minimumCostPath[0][0] = costMatrix[0][0];
for (int i = 1; i <= m; i++) {
minimumCostPath[i][0] = minimumCostPath[i - 1][0] + costMatrix[i][0];
}
for (int j = 1; j <= n; j++) {
minimumCostPath[0][j] = minimumCostPath[0][j - 1] + costMatrix[0][j];
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
minimumCostPath[i][j] = costMatrix[i][j]
+ minimum(minimumCostPath[i - 1][j - 1],
minimumCostPath[i - 1][j],
minimumCostPath[i][j - 1]);
}
}
return minimumCostPath[m][n];
}
public static int minimum(int a, int b, int c) {
return Math.min(a, Math.min(b, c));
}
public static void main(String[] args) {
int[][] costMatrix = { { 3, 2, 8 }, { 1, 9, 7 }, { 0, 5, 2 }, {6, 4, 3} };
System.out.println("Minimum cost: " + minimumCostPathDP(costMatrix, 3, 2));
}
}
Order of the Algorithm
Time Complexity is O(mn)
Space Complexity is O(mn)
