Minimum Depth of a Binary Tree
Given a binary tree, find the minimum depth of the tree.
Minimum depth of a binary tree is the length of the shortest path of all paths from root to any leaf.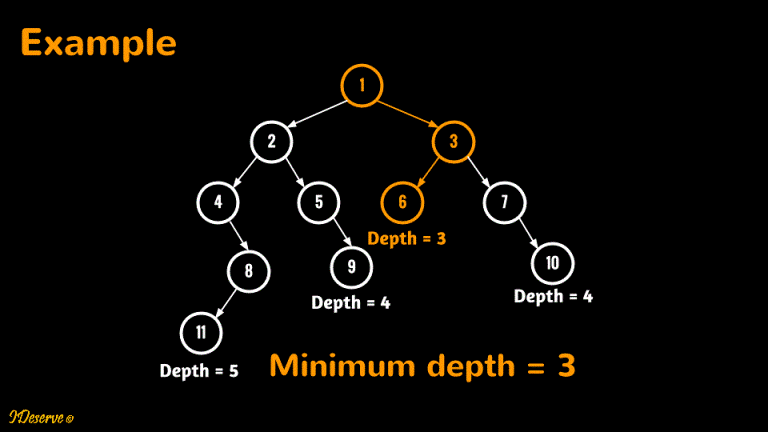
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
1: If root is null, return 0.
2: If root is a leaf, return 1.
3: If left node of root is not null, recursively call getMinDepth to get leftDepth, else set leftDepth to MAX_VALUE
4: If right node of root is not null, recursively call getMinDepth to get rightDepth, else set rightDepth to MAX_VALUE
5: Return 1 + min of leftDepth or rightDepth
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given a binary tree, find the minimum depth of the tree.
* Minimum depth of a binary tree is the length of the shortest
* path of all paths from root to any leaf.
*
* @author Saurabh
*/
public class BinaryTreeMinDepth {
private TreeNode root;
public int getMinDepth() {
return getMinDepth(root);
}
private int getMinDepth(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
int leftDepth = root.left != null ? getMinDepth(root.left) : Integer.MAX_VALUE;
int rightDepth = root.right != null ? getMinDepth(root.right) : Integer.MAX_VALUE;
return 1 + Math.min(leftDepth, rightDepth);
}
public void createSampleTree() {
root = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
TreeNode n9 = new TreeNode(9);
TreeNode n10 = new TreeNode(10);
TreeNode n11 = new TreeNode(11);
root.left = n2;
root.right = n3;
n2.left = n4;
n2.right = n5;
n3.left = n6;
n3.right = n7;
n4.right = n8;
n5.right = n9;
n7.right = n10;
n8.left = n11;
}
public static void main(String[] args) {
BinaryTreeMinDepth tree = new BinaryTreeMinDepth();
tree.createSampleTree();
System.out.println("Min Depth " + tree.getMinDepth());
}
}
class TreeNode {
int data;
TreeNode left;
TreeNode right;
public TreeNode(int data, TreeNode left, TreeNode right) {
super();
this.data = data;
this.left = left;
this.right = right;
}
public TreeNode() {
super();
}
public TreeNode(int data) {
super();
this.data = data;
}
}
Order of the Algorithm
Time Complexity is O(n)
