Print a Matrix Diagonally
Given a matrix of mxn dimensions, print the elements of the matrix in diagonal order.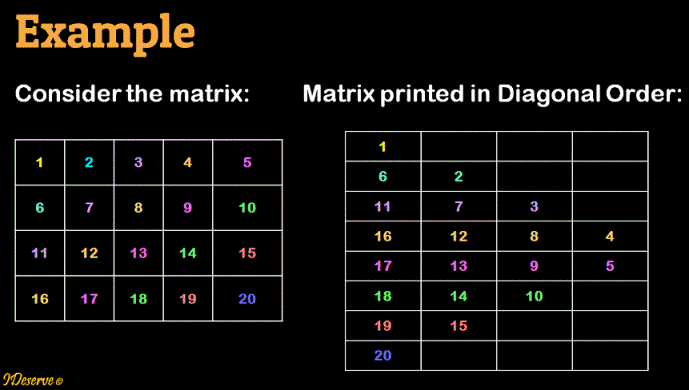
Please check out the video below for detailed explanation of the algorithm with animations.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
rowCount = number of rows
columnCount = number of columns
Then, number of diagonals will be = rowCount + columnCount - 1 as depicted in the diagram below.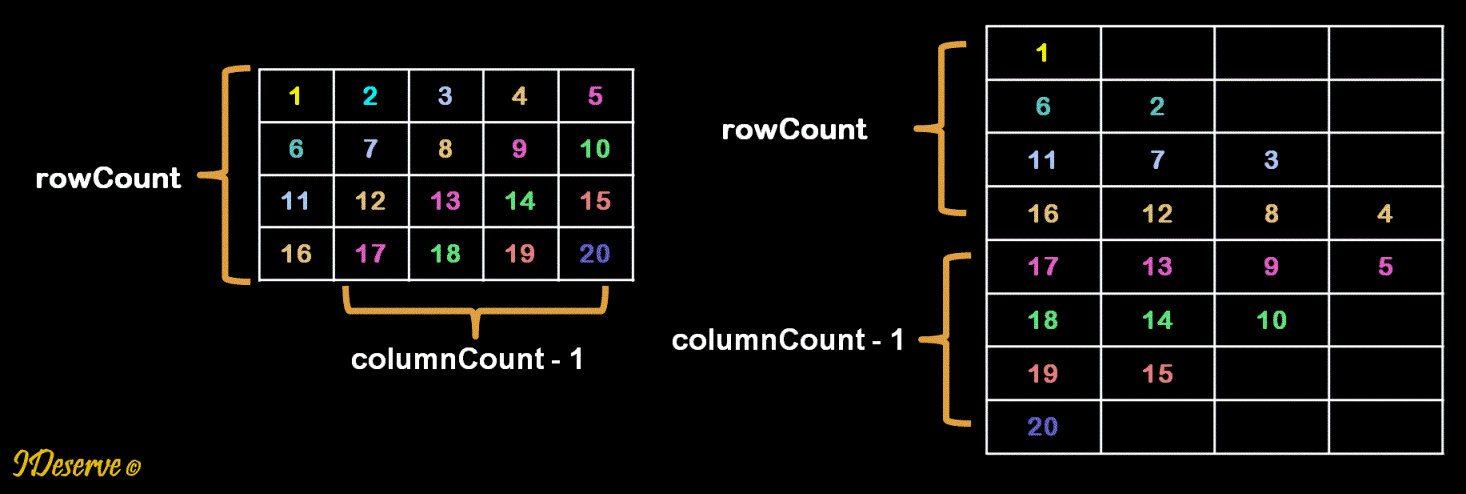
Step 1: Print first rowCount diagonals
Print diagonals that start from the first column
elements.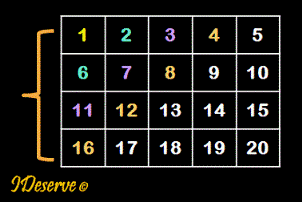
Step 2: Print next columnCount - 1 diagonals
Print diagonals that start from the last row
elements.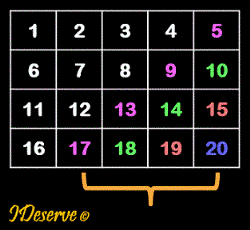
Step 1 details: Print first rowCount diagonals
Iterate to print diagonals from row k = 0 to rowCount - 1.
1: Start with row = k and col = 0
2: Print the element matrix[row][col]
3: Decrement row by 1, increment col by 1 till row >= 0 and col < columnCount
Step 2 details: Print next columnCount - 1 diagonals
Iterate to print diagonals from column k = 1 to columnCount - 1
1: Start with last row, row = rowCount - 1 and col = k
2: Print the element matrix[row][col]
3: Decrement row by 1, increment col by 1 till row >= 0 and col < columnCount
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
import java.util.Arrays;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given a matrix of mxn dimensions, print the elements of the matrix
* in diagonal order.
*
* @author Saurabh
*/
public class PrintMatrixDiagonally {
public static void printMatrixDiagonally(int[][] matrix) {
int row, col;
int rowCount = matrix.length;
int columnCount = matrix[0].length;
for (int k = 0; k < rowCount; k++) {
for (row = k, col = 0; row >= 0 && col < columnCount; row--, col++) {
System.out.print(matrix[row][col] + " ");
}
System.out.println();
}
for (int k = 1; k < columnCount; k++) {
for (row = rowCount - 1, col = k; row >= 0 && col < columnCount; row--, col++) {
System.out.print(matrix[row][col] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int row = 4, col = 5;
int k = 1;
int matrix[][] = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
matrix[i][j] = k++;
}
}
System.out.println("Input Matrix");
for (int i = 0; i < matrix.length; i++) {
System.out.println(Arrays.toString(matrix[i]));
}
System.out.println("\nPrinting Matrix Diagonally");
printMatrixDiagonally(matrix);
}
}
Order of the Algorithm
Time Complexity is O(mn)
Space Complexity is O(1)
