Remove all nodes which lie on path having sum less than k
Given a binary tree, remove all nodes which lie on path having sum less than k.
For example, consider the following binary tree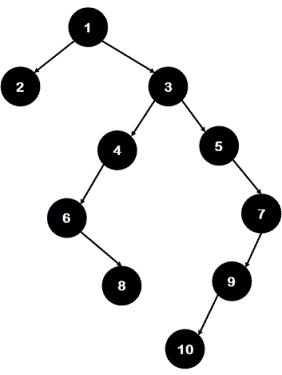
If k=4, after removing all nodes which lie on path having sum less than 4, tree looks like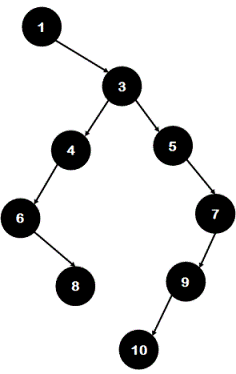
If k=23, after removing all nodes which lie on path having sum less than 23, tree looks like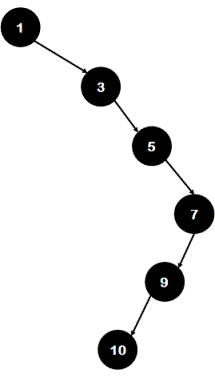
Video coming soon!
Subscribe for more updates
Algorithm/Insights
It is recommended to go through Post-order Traversal of a binary tree first because deleting nodes of a binary tree is done in bottom-up manner by first deleting children and then parent.
While traversing down we pass sum as a parameter which is the sum of all the nodes on the current path including the current node.
Recursively traverse left and right subtrees passing the sum.
Once we reach a leaf node, we check if its path sum is less than k. If it is, then return null.
While backtracking from recursive steps, find maximum of left and right path sum. If the maximum sum becomes less than k, then we delete the current node by setting it to null.
Please note that by the time we come to delete a node, its children would have already been deleted and hence the current node which we will be deleting will be a leaf node.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Remove all nodes which lie on path having sum less than k.
*
* @author Saurabh
*/
public class Tree {
private Node root;
/*
* Create a sample tree
*
* 1
* / \
* 2 3
* / \
* 4 5
* / \
* 6 7
* \ /
* 8 9
* /
* 10
*
*/
public void createSampleTree() {
root = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
Node n4 = new Node(4);
Node n5 = new Node(5);
Node n6 = new Node(6);
Node n7 = new Node(7);
Node n8 = new Node(8);
Node n9 = new Node(9);
Node n10 = new Node(10);
root.left = n2;
root.right = n3;
n3.left = n4;
n3.right = n5;
n4.left = n6;
n5.right = n7;
n6.right = n8;
n7.left = n9;
n9.left = n10;
}
public void deleteKLessPath(int k) {
int sum[] = new int[1];
deleteKLessPath(this.root, sum, k);
if (sum[0] < k)
root = null;
}
public Node deleteKLessPath(Node node, int[] sum, int k) {
if (node == null)
return null;
int[] ls = new int[1];
int[] rs = new int[1];
ls[0] = rs[0] = sum[0] + node.data;
node.left = deleteKLessPath(node.left, ls, k);
node.right = deleteKLessPath(node.right, rs, k);
sum[0] = ls[0] > rs[0] ? ls[0] : rs[0];
if (sum[0] < k) {
node = null;
}
return node;
}
/*
* Preorder traversal
*/
public void printPreorder() {
printPreorder(root);
}
private void printPreorder(Node root) {
if(root == null) {
return;
}
System.out.print(root.data+ " ");
printPreorder(root.left);
printPreorder(root.right);
}
public static void main(String[] args) {
Tree tree = new Tree();
tree.createSampleTree();
tree.deleteKLessPath(23);
tree.printPreorder();
}
}
class Node {
int data;
Node left;
Node right;
public Node(int data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
public Node(int data) {
this.data = data;
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
