Set Partition Problem | Recursion
Given a set, find out if it can be partitioned into two disjoint subsets such that sum of the elements in both these subsets is equal. Intersection of disjoint sets should be null and union should be the complete set.
For set {15,5,15,20,45}, sets {15,5,15} and {20,45} are valid disjoint sets. Also sets {15,5,45} and {15, 20} are valid disjoint sets. But sets {15,5,45,20} and {20,45} are not valid disjoint sets since element 20 is present in both of these subsets.
Coming back to the problem of finding two disjoint sets with equal sums, an example for that could be subsets {15,15,20} and {5,45} for set {15,5,15,20,45}. Sum of elements in both of these subsets is 50. Therefore, the output returned by the program should be 'True'.
Output returned by the program should be 'false' for the set {21,33,37,2}. You can verify that, this set cannot be partitioned into any valid combination of two disjoint subsets such that sum of elements in these subsets is equal.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
First simple idea that we are going to use here is that if sum of all elements in the given set is an odd number say '2n+1', then the best we might be able to do is to partition the given set into two subsets - one with sum 'n' and another with sum 'n+1'. In other words, if sum of all the elements in given set is odd, there is no way the set can be partitioned into two subsets with equal sum and therefore we return 'false' in this case..
Now if the sum of all elements in the given set is an even number say '2n', then all we need to do is to find out a subset say 'S1' of the given set such that sum of elements in that subset is 'n'. The remaining subset(obtained by excluding elements in 'S1') then is guaranteed to have sum = 'n'. For example, the sum of all elements for this set {15,5,15,20,45} is 100. And the subset {5,45} has sum = 50. Now the remaining subset obtained by excluding elements 5 and 45 is {15,15,20} which also has sum = 50.
Notice how we have reduced the original problem into the problem of finding a subset with sum = 'n' when sum of all elements in given set is '2n'. Let's try to solve this modified problem now.
For each element in the set say 'current element', we test for two conditions:
1. If the subset with sum = 'n' could be obtained by including the 'current element'.
2. If the subset with sum = 'n' could be obtained by excluding the 'current element'.
If any of these two conditions is true, we return true.
In the first case, since we are trying to find the subset with sum = 'n' by including the 'current element', we reduce the sum 'n' by value of 'current element' and find out if we can get a subset with sum = 'n - value of current element' from remaining elements of the set.
In the second case, since we are excluding the 'current element' from subset, we try to find out the subset with sum = 'n' from remaining elements of the set.
These two conditions can be tested using recursive calls. If the function call - 'partitionPossible(int requiredSum, int currIndex, int[] set)' is made to check if there is any subset with sum = 'requiredSum' in set(int[] set) with elements starting from 'currIndex' then to test condition #1 we call 'partitionPossible(requiredSum - set[currIndex], currIndex+1, set)' and to test condition #2 we call 'partitionPossible(requiredSum, currIndex+1, set)'.
The base cases for this recursion would be -
1.If the requiredSum is '0' then return 'true'. This is because we can always find an empty subset which would have sum = 0.
2.If requiredSum is not '0' and there are no more elements to look at in the set, that is 'currIndex = set.length' then return 'false'.
For finding out if there is any subset with sum = 50 in the set {15,5,15,20,45}, generated recursion tree using function calls 'partitionPossible' is shown below. The recursion tree is partial recursion tree. Including element at 'currIndex' takes the current state to its left child state and excluding element at 'currIndex' takes it to its right child state.
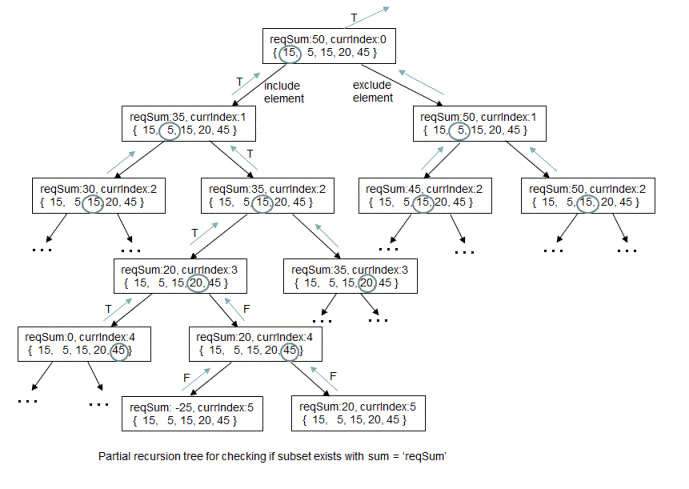
You can observe in the recursion tree how including elements at currIndex = 0, 2 and 3 results in subset with sum = 50.
This path would be left-right-left-left branches from the starting state.
As can be easily observed, the time complexity of this algorithm is O(2^n) and space complexity is O(1). For implementation details of this algorithm, check out function 'partitionPossible(int requiredSum, int currIndex, int[] set)' in code snippet. Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Recursive O(2^n) solution to find out if given set can be partitioned into two disjoint subsets such that -
* sum of the elements in both these subsets is equal.
* @author Nilesh
*/
public class PartitionProblem
{
// find out if there is any subset having sum = requiredSum in given set
private boolean partitionPossible(int requiredSum, int currIndex, int[] set)
{
// there is always an empty subset which gives sum of 0
if (requiredSum == 0)
{
return true;
}
// if we looked at all elements
// and still did not find any subset which has sum = requiredSum
if (currIndex == set.length)
{
return false;
}
/*
* See if there is any subset possible with sum = requiredSum.
*
* When looking at the current element, there are two possibilities
* 1. The element might be present in the subset we are looking for.
* 2. The element might be absent from the subset we are looking for.
*
* We don't know for sure if the subset we are looking for has current element in it
* Therefore, we test for both cases(case #1 and case #2) using following recursive calls
*
* When we choose to include the current element in the subset,
* required sum would be decremented by value of this current element.
*
* When we choose to exclude the current element from the subset,
* required sum would remain the same.
*/
return (
partitionPossible(requiredSum-set[currIndex], currIndex+1, set) ||
partitionPossible(requiredSum, currIndex+1, set)
);
}
public boolean partitionExists(int[] set)
{
int sum = 0;
for (int i = 0; i < set.length; i++)
{
sum += set[i];
}
/*
* if sum of all the elements in given set is odd,
* there is no way they can be partitioned to have equal sum for both partitions
*/
if ((sum % 2) != 0)
{
return false;
}
// else we just need to find a subset which has sum = (sum of all elements in the set)/2
return partitionPossible(sum/2, 0, set);
}
public static void main(String[] args)
{
PartitionProblem solution = new PartitionProblem();
int[] set = {15,5,15,20,45};
System.out.println(solution.partitionExists(set));
}
}
Order of the Algorithm
Time Complexity is O(2^n)
Space Complexity is O(1)
