Total number of possible Binary Search Trees with 'n' keys
How many structurally unique binary search trees(BSTs) are possible that store 'n' distinct values?
For example, if n = 3 then there are total of 5 unique BSTs possible as shown below. For ease of explanation, we would be using values from 1 to 'n' for 'n' distinct keys.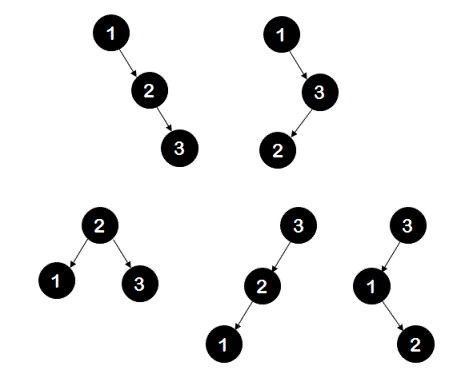
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
To find out the total number of BSTs with 'n' distinct keys, we first assume without loss of generality that the distinct keys used would be from 1 to 'n'. Now using this assumption, we break down the given problem as :
Total number of BSTs for 'n' distinct keys = total number of BSTs with '1' as root + total number of BSTs with '2' as root + ... + total number of BSTs with 'n' as root
Now we try to find out the value of each term on the right hand side of above equation - total number of BSTs with number 'i' as root? We have 'n' distinct keys and we have to make number 'i' as the root of these BSTs. In this case there would be (i-1) distinct values which would go in left sub-trees of BSTs with 'i' as their root and there would be (n-i) distinct values which would go in right sub-trees of BSTs with 'i' as their root. Because left sub-trees of these BSTs formed by (i-1) distinct keys are independent of the right sub-trees of these BSTs formed by (n-i) distinct keys, we can say that the total number of BSTs with 'i' as their root = total number of BSTs with (i-1) distinct keys*total number of BSTs with (n-i) distinct keys.
Notice how we have re-structured given original problem in terms of similar sub-problems. If f(n) denotes the total number of BSTs for 'n' distinct keys then we can re-write f(n) as -
f(n) = total number of BSTs with '1' as root + total number of BSTs with '2' as root + ... + total number of BSTs with 'n' as root
= f(0)f(n-1) + f(1)f(n-2) + f(2)f(n-3) + ... + f(n-2)f(1) + f(n-1)f(0)
For this recurrence relation, base cases are defined as f(0) = 1 and f(1) = 1, since number of BSTs possible with 0 or 1 distinct keys is 1. Notice that many of the terms like f(n-1), f(n-2) in above equation are re-computed. In fact half of the terms in above equation would be computed twice. To avoid these redundant computations, we store the computed values in an array indexed by 'i' and re-use these if required. Please checkout function int computePossibilities(int n, int[] solutions) in code snippet which implements this recurrence relation while storing intermediate results.
The time complexity of this algorithm is O(n^2). This is because f(n) makes 2*(n-1) recursive calls, then f(n-1) makes 2*(n-2) recursive calls and so on. Total number of recursive calls made would be 2(n-1 + n-2 + n-3 + ... + 1) which is O(n^2) recursive calls. Note that because we are storing the intermediate results, though each f(i) occurs twice while evaluating f(n), we need to compute f(i) only once which avoids exponential running time for this algorithm.
Please check out the video for an illustrative explanation. Feel free to add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Total number of possible Binary Search Trees with 'n' keys.
* @author Nilesh
*/
public class NumberOfUniqueBSTs
{
/*
* Total number of BSTs for 'n' distinct keys = total number of BSTs with '1' as root + total number of BSTs with '2' as root
* + ... + total number of BSTs with 'n' as root
*
* Total number of BSTs with 'i' as the root = (Total number of BSTs with 'i-1' distinct keys)*(Total number of BSTs with 'n-i' distinct keys)
*/
// n is input and 'solutions' array stores the intermediate results. All values are initialized to -1
public int computePossibilities(int n, int[] solutions)
{
// base case
if ((n == 1) || (n == 0)) return 1;
int numAllPossibleBSTs = 0;
// summation of total number of BSTs possible with each value of 'i' as the root
for (int i = 1; i <= n; i++)
{
if (solutions[i-1] == -1)
solutions[i-1] = computePossibilities(i-1, solutions); // compute all possible BSTs in its left-subtree
if (solutions[n-i] == -1)
solutions[n-i] = computePossibilities(n-i, solutions); // compute all possible BSTs in its right-subtree
numAllPossibleBSTs += solutions[i-1]*solutions[n-i]; // multiply these two values and add to total
}
return numAllPossibleBSTs;
}
public int numTrees(int n)
{
int[] solutions = new int[n+1];
for (int i = 0; i <= n; i++)
solutions[i] = -1;
return computePossibilities(n, solutions);
}
public static void main(String[] args)
{
NumberOfUniqueBSTs solution = new NumberOfUniqueBSTs();
System.out.print("Total number of BSTs possible for 3 distinct keys: "+solution.numTrees(3));
System.out.print("\n\nTotal number of BSTs possible for 5 distinct keys: "+solution.numTrees(5));
}
}
Order of the Algorithm
Time Complexity is O(n^2)
Space Complexity is O(n)
