AVL tree | Insertion
Write a program to insert given key into the given AVL tree while maintaining height balance of the AVL tree. You might want to check out this previous post which covers the basics of AVL trees.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
We will try to understand this algorithm using an example but before that let's go over the major steps of this insertion algorithm. Note that this algorithm is a bottom-up algorithm and hence height restoration of the tree proceeds from leaves to root.
This algorithm is basically a modification of the usual BST insertion algorithm. The steps of this algorithm are -
1. Use general BST insertion algorithm to insert given key into the AVL tree.
2. After insertion, update the height of the current node of the AVL tree.
3. Now check the 'balance' at the current node by getting the difference of height of left sub-tree and height of right sub-tree.
3a. If 'balance' > 1 then that means the height of the left sub-tree is greater than the height of the right sub-tree. This indicates left-left or left-right case(discussed in the previous post). To confirm if this is left-left or left-right case, value of current node's left child is compared against the inserted key. If key is less than the value of current node's left child then that confirms left-left case and we perform a right rotation at current node. If key is greater than the value of current node's left child then that confirms left-right case and we need to perform two rotations in this case. First left rotation at the current node's left child and then the right rotation at the current node itself. Though the previous post has discussed these scenarios, we will go through an example to make this more clear.
3b. If 'balance' < -1 then that means the height of the right sub-tree is greater than the height of the left sub-tree. This indicates right-right or right-left case(discussed in the previous post). To confirm if this is a right-right or right-left case, value of current node's right child is compared against the inserted key. If key is greater than the value of current node's right child then that confirms right-right case and we perform a left rotation at the current node. If key is less than the value of current node's right child then that confirms right-left case and we need to perform two rotations in this case. First right rotation at the current node's right child and then the left rotation at the current node itself.
Example walk-through: Let's insert key sequence [0,1,2,3,4,6,5] into an AVL tree starting with empty AVL tree.
1. Insertion of key 0 - a tree with a single node with value 0 is initialized.
tree: 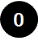
2. Insertion of key 1 - a new node with value 1 is created. This node 1 becomes right child of node 0.
tree: 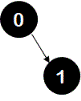
3. Insertion of key 2 - a new node with value 2 is created. This new node becomes right child of node 1.
tree: 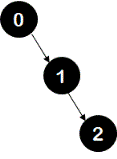
This tree is not balanced at node 0. This is a right-right case and hence a left rotation is done at node 0.
updated tree: 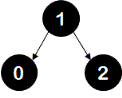
4. Insertion of key 3 - a new node with value 3 is created. This new node becomes right child of node 2.
tree: 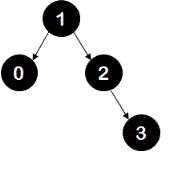
5. Insertion of key 4 - a new node with value 4 is created. This new node becomes right child of node 3.
tree: 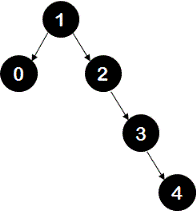
This tree is unbalanced at node 2 with the right-right case and hence left rotation is done at node 2.
update tree: 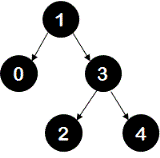
6. Insertion of key 6 - a new node with value 6 is created. This new node becomes right child of node 4.
tree: 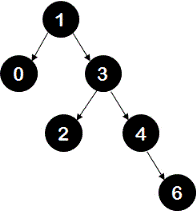
Now note that, at node 1, height of right sub-tree is 3 and the height of left sub-tree is 1. Hence there is an unbalance with the right-right case. To restore balance, a left rotation is done at node 1.
update tree: 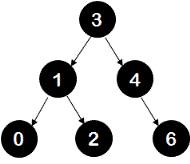
7. Insertion of key 5 - a new node with value 5 is created. This new node becomes left child of node 6.
tree: 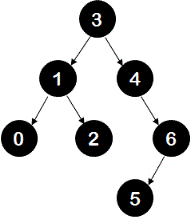
This tree is unbalanced at node 4 with the right-left case. Hence there are two rotations required. First the right rotation at node 6 and then the left rotation at node 4.
Right rotation at node 6: 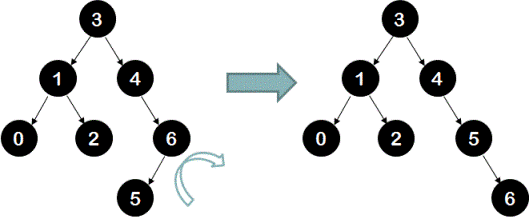
Left rotation at node 4: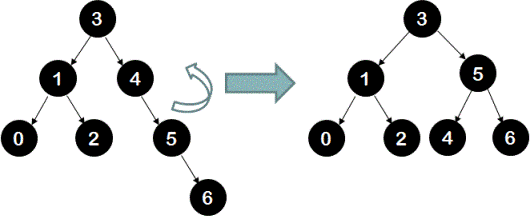
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* AVL Tree insertion algorithm with required rotations for balancing.
* @author Nilesh
*/
public class AVLTree
{
private class QueueNode
{
AVLTreeNode treeNode;
int level;
QueueNode(AVLTreeNode treeNode, int level)
{
this.treeNode = treeNode;
this.level = level;
}
}
private class AVLTreeNode
{
int data;
AVLTreeNode left;
AVLTreeNode right;
int height;
AVLTreeNode(int data)
{
this.data = data;
this.height = 1;
}
}
AVLTreeNode root;
// default value for root node is 9
AVLTree()
{
this.root = new AVLTreeNode(9);
}
AVLTree(int rootValue)
{
this.root = new AVLTreeNode(rootValue);
}
int getHeight(AVLTreeNode node)
{
if (node == null)
return 0;
return node.height;
}
void updateHeight(AVLTreeNode node)
{
if (node == null) return;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
AVLTreeNode rotateRight(AVLTreeNode node)
{
if (node == null) return node;
AVLTreeNode beta = node.left;
AVLTreeNode t2 = beta.right;
beta.right = node;
node.left = t2;
// we first need to update the height of node because height of beta uses height of node
updateHeight(node);
// now we update height of beta
updateHeight(beta);
return beta;
}
AVLTreeNode rotateLeft(AVLTreeNode node)
{
if (node == null) return node;
AVLTreeNode beta = node.right;
AVLTreeNode t2 = beta.left;
beta.left = node;
node.right = t2;
// we first need to update the height of node because height of beta uses height of node
updateHeight(node);
// now we update height of beta
updateHeight(beta);
return beta;
}
int getBalance(AVLTreeNode node)
{
if (node == null)
{
return 0;
}
int balance;
balance = getHeight(node.left) - getHeight(node.right);
return balance;
}
int getMinValue(AVLTreeNode node)
{
// though this case should not be hit ever for the usecase this function is employed for
if (node == null) return Integer.MIN_VALUE;
// if this is the left-most node
if (node.left == null) return node.data;
return getMinValue(node.left);
}
private AVLTreeNode insert(AVLTreeNode node, int key)
{
// do usual BST insertion first
if (node == null)
{
return new AVLTreeNode(key);
}
if (key < node.data)
{
node.left = insert(node.left, key);
}
else if (key > node.data)
{
node.right = insert(node.right, key);
}
else
{
return node;
}
// now update the height of the node
updateHeight(node);
// check the balance at this node and perform rotations accordingly
int balance = getBalance(node);
if (balance > 1) // indicates either left-left or left-right case
{
if (key < node.left.data) // confirms left-left case
{
node = rotateRight(node);
}
else // confirms left-right case
{
node.left = rotateLeft(node.left);
node = rotateRight(node);
}
}
else if (balance < -1) // indicates either right-right or right-left case
{
if (key > node.right.data) // confirms right-right case
{
node = rotateLeft(node);
}
else // confirms right-left case
{
node.right = rotateRight(node.right);
node = rotateLeft(node);
}
}
return node;
}
public void insert(int key)
{
root = insert(this.root, key);
return;
}
public void printTreeLevelOrder()
{
if (root == null) return;
LinkedList queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentNode = (QueueNode) queue.remove();
if (currentNode.level > maxLevelVisited)
{
maxLevelVisited = currentNode.level;
System.out.print("\nlevel-" + currentNode.level + " nodes: ");
}
System.out.print(" " + currentNode.treeNode.data);
if (currentNode.treeNode.left != null)
{
queue.add(new QueueNode(currentNode.treeNode.left, currentNode.level + 1));
}
if (currentNode.treeNode.right != null)
{
queue.add(new QueueNode(currentNode.treeNode.right, currentNode.level + 1));
}
}
}
public static void main(String[] args)
{
AVLTree tree = new AVLTree(0);
tree.insert(1);
tree.insert(2);
tree.insert(3);
tree.insert(4);
tree.insert(6);
tree.insert(5);
tree.printTreeLevelOrder();
}
}
Order of the Algorithm
Time Complexity is O(logn)
Space Complexity is O(1)
