Check if a binary tree is sub-tree of another binary tree in space O(1)
Given two binary trees t1 and t2, check if tree t2 is sub-tree of tree t1. A sub-tree of tree T1 is a tree T2 having any one of the nodes 'n' and all the descendants of node 'n'.
In the following example, the middle tree - 'Tree_1' is sub-tree of leftmost tree - 'Tree_0'. Note that the rightmost tree - 'Tree_2' is not a sub-tree of 'Tree_0' because of the absence of node 8.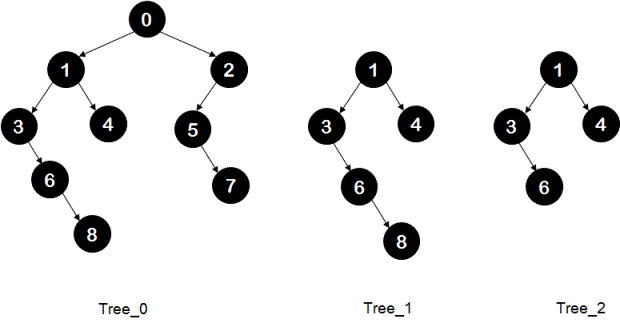
Video coming soon!
Subscribe for more updates
Algorithm/Insights
If function checkIfSubtree(TreeNode bigTreeRoot, TreeNode smallTreeRoot) implements this algorithm then the steps of this intuitive algorithm are as following -
1. If 'smallTreeRoot is equal to null' then return true since 'null' tree is sub-tree for any tree.
2. If condition #1 is not true then check if 'bigTreeRoot is equal to null'. If it is then return false since null tree cannot have any sub-tree except null tree for which we have already checked in #1.
3. If both conditions #1 and #2 are not true then check if value of smallTreeRoot is equal to value of bigTreeRoot.
4. If condition #3 evaluated to true then we check if left sub-tree of smallTreeRoot exactly matches to left sub-tree of bigTreeRoot and right sub-tree of smallTreeRoot exactly matches to right sub-tree of bigTreeRoot. If both sub-trees match then we return true since we know that smallTree is now a sub-tree of bigTree.
5. If either #3 or #4 evaluate to false then we check if left sub-tree of bigTreeRoot contains smallTree or right sub-tree of bigTreeRoot contains smallTree. For checking this we simply make recursive calls.
Time complexity for this approach is O(n^2) and space complexity for this approach is O(1).
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Check if tree 't2' is sub-tree of tree 't1'
* @author Nilesh
*/
public class CheckIfSubtree {
class TreeNode
{
TreeNode left;
TreeNode right;
char key;
public TreeNode(char key)
{
this.key = key;
}
}
TreeNode root;
/*
0
1 2
3 4 5
6 7
8
*/
private TreeNode createBigTree()
{
TreeNode n0 = new TreeNode('0');
TreeNode n1 = new TreeNode('1');
TreeNode n2 = new TreeNode('2');
TreeNode n3 = new TreeNode('3');
TreeNode n4 = new TreeNode('4');
TreeNode n5 = new TreeNode('5');
TreeNode n6 = new TreeNode('6');
TreeNode n7 = new TreeNode('7');
TreeNode n8 = new TreeNode('8');
n0.left = n1;
n0.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.right = n6;
n5.right = n7;
n6.right = n8;
root = n0;
return n0;
}
/*
1
3 4
6
8
*/
private TreeNode createSmallTree()
{
TreeNode n1 = new TreeNode('1');
TreeNode n3 = new TreeNode('3');
TreeNode n4 = new TreeNode('4');
TreeNode n6 = new TreeNode('6');
TreeNode n8 = new TreeNode('8');
n1.left = n3;
n1.right = n4;
n3.right = n6;
n6.right = n8;
root = n1;
return n1;
}
private boolean completeMatch(TreeNode bigTreeRoot, TreeNode smallTreeRoot)
{
if ((bigTreeRoot == null) && (smallTreeRoot == null))
{
return true;
}
if ((bigTreeRoot == null) || (smallTreeRoot == null))
{
return false;
}
if (bigTreeRoot.key == smallTreeRoot.key)
{
return completeMatch(bigTreeRoot.left, smallTreeRoot.left) && completeMatch(bigTreeRoot.right, smallTreeRoot.right);
}
return false;
}
public boolean checkIfSubtree(TreeNode bigTreeRoot, TreeNode smallTreeRoot)
{
if (smallTreeRoot == null)
{
return true;
}
if (bigTreeRoot == null)
{
return false;
}
if (bigTreeRoot.key == smallTreeRoot.key)
{
if (completeMatch(bigTreeRoot, smallTreeRoot))
{
return true;
}
}
return checkIfSubtree(bigTreeRoot.left, smallTreeRoot) || checkIfSubtree(bigTreeRoot.right, smallTreeRoot);
}
public static void main(String[] args)
{
/*
0
1 2
3 4 5
6 7
8
*/
CheckIfSubtree bigTree = new CheckIfSubtree();
bigTree.createBigTree();
/*
1
3 4
6
8
*/
CheckIfSubtree smallTree = new CheckIfSubtree();
smallTree.createSmallTree();
System.out.println("If small tree is sub-tree of big tree: " + bigTree.checkIfSubtree(bigTree.root, smallTree.root));
}
}
Order of the Algorithm
Time Complexity is O(n^2)
Space Complexity is O(1)
