Binary Search tree | Insertion and Search
Write a program to insert a given key in the given binary search tree(BST). Given BST should remain BST even after insertion of the key. Also write a program to search a node with given key value in the BST.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
In the BST insertion algorithm, every new key is inserted as a leaf node. The algorithm basically searches for the correct position of the new node in the BST.
If insert(currentNode, key) is called then -
1. If currentNode is null, then either this is an empty tree or we have reached the correct position in the tree for this key.
We create a new node with this key and make currentNode reference point to this new node.
2. If the value of key is less than currentNode value, then we know that correct position for this key is in the left sub-tree of currentNode. We also know that the left sub-tree would be modified after inserting this key. Therefore we make a recursive call as - currentNode.left = insert(currentNode.left, key)
3. If the value of key is greater than currentNode value, then we know that correct position for this key is in the right sub-tree of currentNode. We also know that the right sub-tree would be modified after inserting this key. Therefore we make a recursive call as - currentNode.right = insert(currentNode.right, key)
4. Insertion of key would be completed in above steps. In this step, we return reference of currentNode to the calling function to make it visible the changes that have occurred in the tree(due to insertion of new key) rooted at currentNode.
Note how this algorithm handles insertion of duplicates keys. If the key value matches the currentNode value, then this algorithm does no action and simply returns reference of currentNode thereby avoiding insertion of duplicate keys.
Following diagram illustrates insertion of key '4' into the BST. 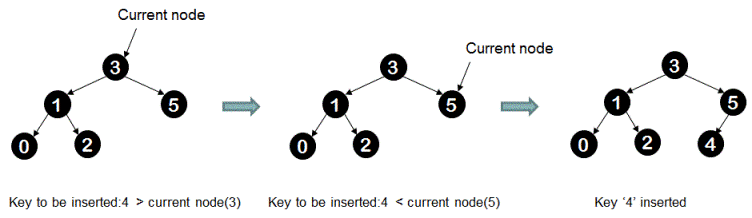
Check out function insert(BinarySearchTreeNode node, int key) in the code snippet for implementation.
BST search algorithm - Search algorithm is very similar to insertion algorithm. If function call - search(currentNode, key) is made for searching key into the tree rooted at currentNode, then
1. If currentNode is null, then we return null since we are searching in an empty tree.
2. If key is equal to the currentNode's value, then we know that we have found the key at this currentNode itself and we return reference to currentNode.
3. If key is less than currentNode's value, we search for key in the left sub-tree.
4. If key is greater than currentNode's value, we search for key in the right sub-tree.
Check out function search(BinarySearchTreeNode node, int key) in the code snippet for implementation.
For both of these algorithms, worst case time complexity would be O(n) and average case time taken would be O(logn).
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Binary Search Tree deletion algorithm.
* @author Nilesh
*/
public class BinarySearchTree
{
private class QueueNode
{
BinarySearchTreeNode treeNode;
int level;
QueueNode(BinarySearchTreeNode treeNode, int level)
{
this.treeNode = treeNode;
this.level = level;
}
}
private class BinarySearchTreeNode
{
int data;
BinarySearchTreeNode left;
BinarySearchTreeNode right;
BinarySearchTreeNode(int data)
{
this.data = data;
}
}
BinarySearchTreeNode root;
// default value for root node is 9
BinarySearchTree()
{
this.root = new BinarySearchTreeNode(9);
}
BinarySearchTree(int rootValue)
{
this.root = new BinarySearchTreeNode(rootValue);
}
private BinarySearchTreeNode search(BinarySearchTreeNode node, int key)
{
if (node == null) // base case
{
return null;
}
BinarySearchTreeNode searchedNode = null;
if (key == node.data) // key found!
{
searchedNode = node;
}
else if (key < node.data) // search key into left sub-tree
{
searchedNode = search(node.left, key);
}
else if (key > node.data) // search key into right sub-tree
{
searchedNode = search(node.right, key);
}
return searchedNode;
}
public BinarySearchTreeNode search(int key)
{
BinarySearchTreeNode searchedNode = search(this.root, key);
if (searchedNode == null)
{
System.out.println("\n\nKey not found!");
}
else
{
System.out.println("\n\nKey found!");
}
return searchedNode;
}
private BinarySearchTreeNode insert(BinarySearchTreeNode node, int key)
{
if (node == null) // base case
{
node = new BinarySearchTreeNode(key);
}
if (key < node.data) // insert key into left sub-tree
{
node.left = insert(node.left, key);
}
else if (key > node.data) // insert key into right sub-tree
{
node.right = insert(node.right, key);
}
return node;
}
public void insert(int key)
{
root = insert(this.root, key);
return;
}
public void printTreeLevelOrder()
{
if (root == null) return;
LinkedList queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentNode = (QueueNode) queue.remove();
if (currentNode.level > maxLevelVisited)
{
maxLevelVisited = currentNode.level;
System.out.print("\nlevel-" + currentNode.level + " nodes: ");
}
System.out.print(" " + currentNode.treeNode.data);
if (currentNode.treeNode.left != null)
{
queue.add(new QueueNode(currentNode.treeNode.left, currentNode.level + 1));
}
if (currentNode.treeNode.right != null)
{
queue.add(new QueueNode(currentNode.treeNode.right, currentNode.level + 1));
}
}
}
public static void main(String[] args)
{
BinarySearchTree tree = new BinarySearchTree(3);
tree.insert(1);
tree.insert(5);
tree.insert(0);
tree.insert(2);
tree.insert(4);
/*
* 3
* 1 5
* 0 2 4
*
*/
System.out.print("BinarySearch tree level order traversal:");
tree.printTreeLevelOrder();
tree.search(3);
}
}
Order of the Algorithm
Time Complexity is O(logn)(Average case)
Space Complexity is O(1)
