Check if a given binary tree is symmetric tree or not
Write a program to check if the given binary tree is symmetric tree or not. A symmetric tree is defined as a tree which is mirror image of itself about the root node. For example, following tree is a symmetric tree.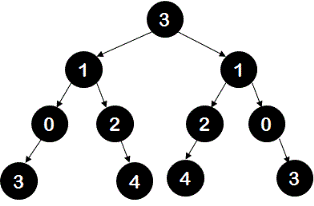
whereas, following tree is not a symmetric tree. 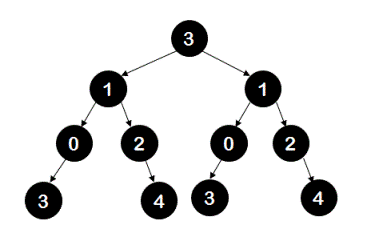
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The algorithm is an implementation of a simple idea that -
1. For given two trees, if both trees are empty then they are mirror images of one another.
Else they have to satisfy following conditions:
2. Root values of both trees have to be same.
3. Left sub-tree of tree1 should be mirror image of right sub-tree of tree2.
4. Right sub-tree of tree1 should be mirror image of left sub-tree of tree2.
Initial call to isSymmetric(TreeNode root1, TreeNode root2) is made with root1 = root and root2 = root.
Time complexity of this algorithm is O(n) since in the worst case each node need to be visited once.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution to check if binary tree is symmetric or not. Uses Pre-order traversal.
* @author Nilesh
*/
public class CheckIfSymmetricBinaryTree
{
class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
0
1 1
3 4 4 3
5 5
*/
private TreeNode createTree()
{
this.root = new TreeNode(0);
TreeNode n10 = new TreeNode(1);
TreeNode n11 = new TreeNode(1);
TreeNode n30 = new TreeNode(3);
TreeNode n31 = new TreeNode(3);
TreeNode n40 = new TreeNode(4);
TreeNode n41 = new TreeNode(4);
TreeNode n50 = new TreeNode(5);
TreeNode n51 = new TreeNode(5);
root.left = n10;
root.right = n11;
n10.left = n30;
n10.right = n40;
n11.right = n31;
n11.left = n41;
n30.left = n50;
n31.right = n51;
return root;
}
private boolean isSymmetric(TreeNode root1, TreeNode root2)
{
if (root1 == null && root2 == null)
{
return true;
}
else if (root1 == null || root2 == null)
{
return false;
}
if (root1.value == root2.value)
{
if (isSymmetric(root1.left, root2.right))
{
return isSymmetric(root1.right, root2.left);
}
}
return false;
}
public boolean isSymmetric(TreeNode root)
{
return isSymmetric(root, root);
}
public static void main(String[] args)
{
CheckIfSymmetricBinaryTree tree = new CheckIfSymmetricBinaryTree();
/*
0
1 1
3 4 4 3
5 5
*/
tree.createTree();
System.out.println("tree is symmetric: "+tree.isSymmetric(tree.root));
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
