Binary Search tree | Deletion
Write a program to delete a given key from the given binary search tree(BST). Given BST should remain BST even after deletion of the given key.
Question Asked in
Ebay
Video coming soon!
Subscribe for more updates
Algorithm/Insights
To delete a node/key from the given binary search tree, we need to consider two cases. First case - if the node to be deleted is a leaf node or has only one child. Second case - if the node to be deleted has both children.
First case:
a. Leaf node deletion: As shown below, to delete node 4 we simply need to make left child of node 5 as null by returning null to the calling function when current node is 4. Calling function would have current node as 5.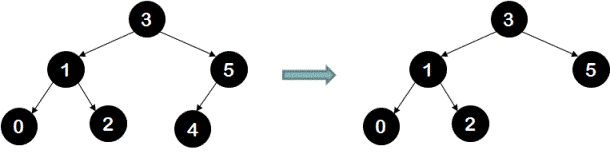
b. Deletion of node with only one child: As shown below, to delete node 5 which has only one child(node 4), we need to return the reference of the child node to the calling function when the current node is 5. In this example, calling function would have current node as 3 and to it we return reference to node 4, effectively deleting node 5. 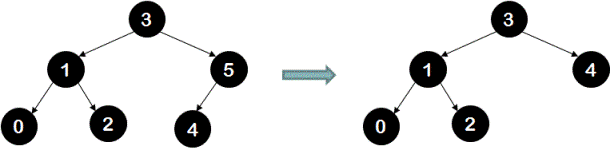
Second case:
Deletion of node which has both children: To delete node 3 from the below tree, what we do is we find out the inorder successor of node 3 (which is node 4), copy its value to the node 3(which needs to be deleted) and then proceed to delete the node 4(inorder successor of node 4). 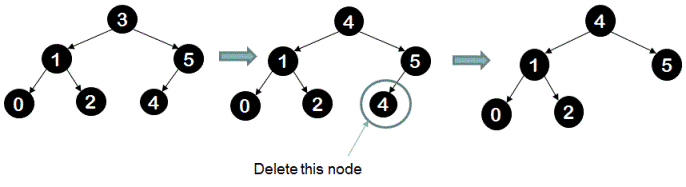
Note that, instead of using inorder successor, we could have used inorder predecessor as well.
In the code section, we have implemented deletion algorithm for the same example discussed in the second case above. In the algorithm implementation, you should be able to notice that handling the case of deletion of node with only one child automatically handles the case of deletion of leaf node.
For this algorithm, worst case time complexity would be O(n) and average case time taken would be O(logn). The space complexity of this algorithm would be O(h) with 'h' again being the depth of the tree since at any point of time maximum number of stack frames that could be present in memory is 'h'.
You can refer to this post for more details about time and space complexity of recursive algorithms.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Binary Search Tree deletion algorithm.
* @author Nilesh
*/
public class BinarySearchTree
{
private class QueueNode
{
BinarySearchTreeNode treeNode;
int level;
QueueNode(BinarySearchTreeNode treeNode, int level)
{
this.treeNode = treeNode;
this.level = level;
}
}
private class BinarySearchTreeNode
{
int data;
BinarySearchTreeNode left;
BinarySearchTreeNode right;
BinarySearchTreeNode(int data)
{
this.data = data;
}
}
BinarySearchTreeNode root;
// default value for root node is 9
BinarySearchTree()
{
this.root = new BinarySearchTreeNode(9);
}
BinarySearchTree(int rootValue)
{
this.root = new BinarySearchTreeNode(rootValue);
}
int getMinValue(BinarySearchTreeNode node)
{
// though this case should not be hit ever for the usecase this function is employed for
if (node == null) return Integer.MIN_VALUE;
// if this is the left-most node
if (node.left == null) return node.data;
return getMinValue(node.left);
}
private BinarySearchTreeNode delete(BinarySearchTreeNode node, int key)
{
// if empty tree or key not found
if (node == null) return null;
if (key < node.data) // search key in left sub-tree
{
node.left = delete(node.left, key);
}
else if (key > node.data) // search key in right sub-tree
{
node.right = delete(node.right, key);
}
else // key to be deleted is equal to node data
{
// one child/no child case
if (node.left == null)
{
node = node.right;
}
else if (node.right == null)
{
node = node.left;
}
// two children case
// copy value of inorder successor into the current node and delete inorder successor
// since right sub-tree would be modified, update node.right
else
{
int inorderSuccessorValue = getMinValue(node.right);
node.data = inorderSuccessorValue;
node.right = delete(node.right, inorderSuccessorValue);
}
}
return node;
}
private BinarySearchTreeNode insert(BinarySearchTreeNode node, int key)
{
if (node == null) // base case
{
return new BinarySearchTreeNode(key);
}
if (key < node.data) // insert key into left sub-tree
{
node.left = insert(node.left, key);
}
else if (key > node.data) // insert key into right sub-tree
{
node.right = insert(node.right, key);
}
else // key already present in BST
{
return node;
}
return node;
}
public void insert(int key)
{
root = insert(this.root, key);
return;
}
public void delete(int key)
{
root = delete(this.root, key);
return;
}
public void printTreeLevelOrder()
{
if (root == null) return;
LinkedList queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentNode = (QueueNode) queue.remove();
if (currentNode.level > maxLevelVisited)
{
maxLevelVisited = currentNode.level;
System.out.print("\nlevel-" + currentNode.level + " nodes: ");
}
System.out.print(" " + currentNode.treeNode.data);
if (currentNode.treeNode.left != null)
{
queue.add(new QueueNode(currentNode.treeNode.left, currentNode.level + 1));
}
if (currentNode.treeNode.right != null)
{
queue.add(new QueueNode(currentNode.treeNode.right, currentNode.level + 1));
}
}
}
public static void main(String[] args)
{
BinarySearchTree tree = new BinarySearchTree(3);
tree.insert(1);
tree.insert(5);
tree.insert(0);
tree.insert(2);
tree.insert(4);
/*
* 3
* 1 5
* 0 2 4
*
*/
System.out.print("BinarySearch tree before deleting any key");
tree.printTreeLevelOrder();
tree.delete(3);
/*
* 4
* 1 5
* 0 2
*
*/
System.out.print("\n\nBinarySearch tree after deleting keys - 3");
tree.printTreeLevelOrder();
}
}
Order of the Algorithm
Time Complexity is O(logn)(Average case)
Space Complexity is O(h) h: height of BST
