Check if two nodes are cousins in a Binary tree
Given two nodes in a binary tree, check if they are cousins.
Two nodes are cousins if:
1: they are not siblings (children of same parent).
2: they are on the same level.
For example, in the following binary tree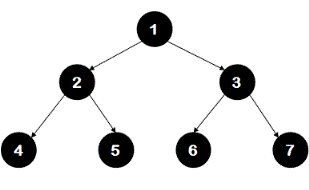
nodes 5 and 6 are cousins but nodes 4 and 5 are not.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
1: If node A == B return false as a node cannot be cousin of itself.
2: Check nodes A and B are not siblings and
3: Check nodes A and B are on same level.
How to find if 2 nodes are siblings:
1. If A and B are left and right children of the root, then they are siblings.
2. Else check Step 1 in left and right subtrees.
3. If the condition in Step 1 is not true for any node, then the nodes are not siblings.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given two nodes in a binary tree, check if they are cousins.
* Two nodes are cousins if:
* 1: they are not siblings.
* 2: they are on the same level.
*
* @author Saurabh
*/
public class Tree {
private Node root;
public void setRoot(Node root) {
this.root = root;
}
/*
* Condition for cousins:
* 1: Given nodes are not siblings.
* 2: Given nodes should be on the same level.
*/
public Boolean isCousin(Node a, Node b) {
// A node cannot be cousin of itself.
if (a == b) {
return false;
}
return (!isSibling(a, b) && getLevel(a) == getLevel(b));
}
public int getLevel(Node a) {
return getLevel(root, a, 1);
}
private int getLevel(Node root, Node a, int currLevel) {
if (root == null)
return 0;
if (root == a)
return currLevel;
int level = getLevel(root.left, a, currLevel + 1);
if (level != 0) {
return level;
} else
return getLevel(root.right, a, currLevel + 1);
}
public boolean isSibling(Node a, Node b) {
return isSibling(root, a, b);
}
private boolean isSibling(Node root, Node a, Node b) {
if (root == null)
return false;
return ((root.left == a && root.right == b) || (root.right == a && root.left == b) ||
isSibling(root.left, a, b) || isSibling(root.right, a, b));
}
public static void main(String[] args) {
Tree tree = new Tree();
/*
* Create a sample tree
*
* 1
* / \
* 2 3
* / \ / \
* 4 5 6 7
*/
Node root = new Node(1);
Node n2 = new Node(2);
Node n3 = new Node(3);
Node n4 = new Node(4);
Node n5 = new Node(5);
Node n6 = new Node(6);
Node n7 = new Node(7);
root.left = n2;
root.right = n3;
n2.left = n4;
n2.right = n5;
n3.left = n6;
n3.right = n7;
tree.setRoot(root);
System.out.println("Nodes " + n5.data + " and " + n6.data + (tree.isCousin(n5, n6) ? " are cousins." : " are not cousins."));
}
}
class Node {
int data;
Node left;
Node right;
public Node(int data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
public Node(int data) {
this.data = data;
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
