Check whether a binary tree is complete or not
Write a program to check if a given binary tree is complete tree or not.
A binary tree is a complete binary tree if all levels of the tree starting from root node level are filled. Only the last level of the tree is allowed to have an incompletely filled state. Also for tree to be a complete binary tree, all nodes should be placed as left as possible. For example, both tree shown below are complete trees. Though the tree on the left-hand side has one of the levels incompletely filled, because it is the last level this tree fulfills conditions for a complete tree.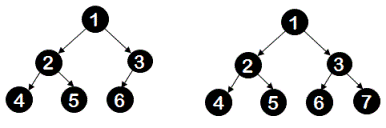
Below shown tree is not a complete binary tree because level-2 (with nodes '4','5' and '6') is incomplete though it is not the last level in the tree.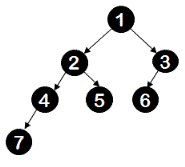
Similarly, below tree is also not a complete binary tree because though all the levels are completely filled except the last level, node 8 must be the left-child of its parent for this tree to be complete binary tree. Otherwise, it violates the condition - all nodes should be placed as left as possible.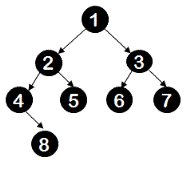
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The idea to solve this problem is simple. We do a usual level order traversal and whenever we see that there is a node which does not have both left and right child, then we set nonFullNodeSeen = true. This indicates that while doing level order traversal, we have seen our first node with either right or left or both children absent. And for a complete binary tree, all the nodes visited during level order traversal after visiting a nonFullNode would be leaf nodes. If this is not true, we return false. For example, in the left-hand side complete tree shown above, once we visit node '3' which is a nonFullNode, the nodes visited after this node are node '4','5' and '6' all of which are leaf nodes.
We also need to check if there is any node with right child but with no left child. In this case, we simply return false.
Please checkout code snippet and algorithm visualization section for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Check if binary tree is a complete tree or not.
* @author Nilesh
*/
public class CompleteBinaryTreeCheck {
class QueueNode
{
TreeNode node;
QueueNode(TreeNode node)
{
this.node = node;
}
}
class TreeNode
{
TreeNode left;
TreeNode right;
int val;
public TreeNode(int x)
{
this.val = x;
}
}
TreeNode root;
/*
1
2 3
4 5 6
*/
private TreeNode createCompleteTree()
{
this.root = new TreeNode(1);
TreeNode n1 = new TreeNode(2);
TreeNode n2 = new TreeNode(3);
TreeNode n3 = new TreeNode(4);
TreeNode n4 = new TreeNode(5);
TreeNode n5 = new TreeNode(6);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
return root;
}
/*
1
2 3
4 5 6
7
*/
private TreeNode createIncompleteTree()
{
this.root = new TreeNode(1);
TreeNode n1 = new TreeNode(2);
TreeNode n2 = new TreeNode(3);
TreeNode n3 = new TreeNode(4);
TreeNode n4 = new TreeNode(5);
TreeNode n5 = new TreeNode(6);
TreeNode n6 = new TreeNode(7);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.left = n6;
return root;
}
public boolean checkIfComplete()
{
if (root == null) return true;
LinkedList<TreeNode> queue = new LinkedList();
boolean nonFullNodeSeen = false;
queue.add(root);
while (!queue.isEmpty())
{
TreeNode currentNode = queue.remove();
if ((currentNode.left != null) && (currentNode.right != null))
{
// there should not be any non-leaf node after first non full-node is seen
if (nonFullNodeSeen)
{
return false;
}
queue.add(currentNode.left);
queue.add(currentNode.right);
}
if ((currentNode.left != null) && (currentNode.right == null))
{
// there should not be any non-leaf node after first non full-node is seen
if (nonFullNodeSeen)
{
return false;
}
// this is the first non-full node seen
nonFullNodeSeen = true;
queue.add(currentNode.left);
}
// this should never be the case for a complete binary tree
if ((currentNode.left == null) && (currentNode.right != null))
{
return false;
}
}
return true;
}
public static void main(String[] args)
{
CompleteBinaryTreeCheck tree = new CompleteBinaryTreeCheck();
tree.createCompleteTree();
System.out.println(tree.checkIfComplete());
tree.createIncompleteTree();
System.out.println(tree.checkIfComplete());
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
