Find height of the binary tree from its parent array representation
Given parent array representation of the tree, find the height of the tree. In this parent array representation, a node would be constructed with values taken from indices of this array. For element parent[i], a node would be constructed with value 'i'. And parent node for this constructed node with value 'i' would be node with value parent[i]. If parent[i] is -1, then we make the node with value 'i' as the root of the tree. For example, for the parent array {3, 5, 0, -1, 5, 3, 0}:
parent[0] = parent[5] = 3, therefore node with value 3 would be parent node for nodes with values 0 and 5.
parent[1] = parent[4] = 5, therefore node with value 5 would be parent node for nodes with values 1 and 4.
parent[2] = parent[6] = 0 implies that node with value 0 would be parant node for nodes with values 2 and 6.
parent[3] = -1 therefore, node 3 would be the root node for this tree.
The complete constructed tree for parent array {3, 5, 0, -1, 5, 3, 0} would look like following: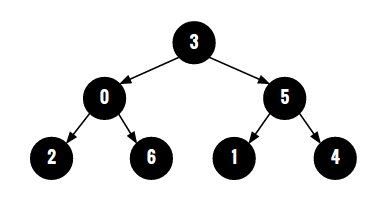
And output of the program should be the height of this tree that is 3.
For parent array {-1, 0, 1, 5, 1, 0}, constructed binary tree would be :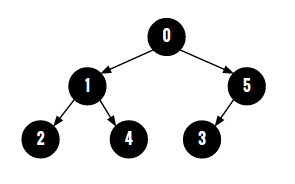
And output of the program should be the height of this tree that is 3.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
There are two main approaches to solve this problem. First very intuitive approach would be to construct the complete tree from its parent array representation and simply compute the height of that tree. We have discussed the solution to constructing a tree from its parent array representation here in this post. This algorithm could be run in O(n) time when the tree is constructed in bottom-up manner.
Now let's look at the approach where we don't need to construct the binary tree to find the height of it from its parent array representation. The steps of this algorithm are as following -
1. Create height array of size same as parent array. For all legal values of 'i' make height[i] = INVALID_HEIGHT. height[i] denotes the height of node with value 'i'.
2. To compute the height for all nodes of this tree, we call computeHeight(i, height, parent) for all values of legal values of 'i'.
3. In computeHeight(i, height, parent) recursive function,
3a. If height[i] is already computed, we return to the calling function.
3b. If parent[i] == -1, then that means this index corresponds to root node. Hence we make height[i] = 1 and return. Note that, as against the conventional notion of height here we have height of root node as minimum and height of leaf node as maximum.
3c. If conditions 3a and 3b are not true, then first we compute the height of the parent node by making a recursive call computeHeight(parent[i], height, parent). This parent height would be used to compute the height of the current node.
3d. Once we compute height of parent node, we compute height of current node with value 'i' as height[i] = 1 + height[parent[i]] and return.
4. After computeHeight() call sequence is complete, we have heights for all tree nodes. Now all we do is scan the height array to find and return the maximum height from this height array.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution to find height of the binary tree from its parent array representation.
* @author Nilesh
*/
public class HeightOfTreeFromParentArray {
final static int INVALID_HEIGHT = -1;
private void computeHeight(int i, int[] height, int[] parent)
{
// height already computed for node with value as index 'i'
if (height[i] != INVALID_HEIGHT)
{
return;
}
// if this is index 'i' corresponds to the root node,
// then make height[i] = 1
if (parent[i] == -1)
{
height[i] = 1;
return;
}
// first compute the height for the parent node
if (height[parent[i]] == INVALID_HEIGHT)
{
computeHeight(parent[i], height, parent);
}
// now compute the height of the current node using height of its parent node
if (height[parent[i]] != INVALID_HEIGHT) // sanity check
{
height[i] = 1 + height[parent[i]];
}
}
public int computeHeight(int[] parent)
{
int[] height = new int[parent.length];
for (int i = 0; i < height.length; i++)
{
height[i] = INVALID_HEIGHT;
}
// compute height for all nodes
for (int i = 0; i < height.length; i++)
{
computeHeight(i, height, parent);
}
// return the maximum of them
int maxHeight = -1;
for (int i = 0; i < height.length; i++)
{
if (height[i] > maxHeight)
{
maxHeight = height[i];
}
}
return maxHeight;
}
public static void main(String[] args)
{
HeightOfTreeFromParentArray solution = new HeightOfTreeFromParentArray();
int[] parent = {3, 5, 0, -1, 5, 3, 0};
/*
3
0 5
2 6 1 4
*/
System.out.println("Height of constructed tree would be: " + solution.computeHeight(parent));
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
