Find the missing number in the increasing sequence
Given an increasing sequence of numbers from 1 to n with only one missing number, how can you find that missing number without traversing the sequence in linear fashion. In other words, time complexity of your algorithm must be less than O(n)?
For example, if the given sequence is 1,2,4,5,6,7,8 then the missing number is 3. If the given sequence is 1,3,4,5 then the missing number is 2. For the input 2,3,4,5 output returned should be 1 as it is the missing number.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
If we traverse the given sequence number by number starting from the element at the 0th index, we can easily tell which number is missing by looking at the difference between the number at index 'i' and number at index 'i-1'. If this difference is greater than 1, we know that we have identified a missing number. For example, for sequence {1,2,3,4,6,7,8}, difference between number 6 and number 4 is 2 and hence we say that missing number is 5. BUT, as per the problem statement we are not supposed to traverse the sequence in linear fashion. Let's look at an optimized approach which runs in log(n) time.
Correctly placed numbers: For a number 'i', if all the 'i-1' numbers appearing before it are present in the given sequence then we say that the number 'i' is correctly placed in the given sequence. Because the given sequence is stored in an array which starts from index 0, we can easily check if a number is correctly placed by checking if its index is equal to the value of that number minus 1. For example, for sequence {1,2,3,4,6,7,8}, if you consider number 4 which is correctly placed, its index is 3 which is 4 minus 1. Same is the case for numbers 1,2 and 3. But for numbers 6,7 and 8 which are not correctly placed(since number 5 which appears before them is missing), their respective indices are not equal to their respective values minus 1.
Idea: Now using the above idea of correctly placed numbers, to find out the missing number we find the first number from the left in the given sequence(say number 'j') which is incorrectly placed. Once we find this number 'j', we know that the missing number must be 'j-1' since number 'j' is the first element from the left which is incorrectly placed in the given sequence.
Algorithm: We find this above defined number 'j' using binary search algorithm. If 'array' stores the given sequence and if function 'findMissingElement(int[] array, int low, int high)' is used to find the missing number in this 'array' with its first element at index 'low' and its last element at index 'high', then the steps used by this function are as following -
1. If low > high, then this is invalid input case. To indicate that, return -1.
2. If low == high, then we have found the first element which is incorrectly placed. Return 'array[high] - 1' in this case.
Step #1 and step #2 are base cases for this binary search. Recursive steps are as following.
3. Calculate mid as (low + high)/2.
a. If array[mid] is correctly placed, then we need to search for the first incorrectly placed element in the higher half of the array(from 'mid + 1' to high). Note that since array[mid] is correctly placed it cannot be the first incorrectly placed element and therefore we exclude it from the search by making low = mid + 1.
b. If array[mid] is incorrectly placed, then we need to search for the first incorrectly placed element in the lower half of the array(from low to mid). Note that since array[mid] could also be the first element which is incorrectly placed, we cannot exclude it from the search and hence we make high = mid(and not 'mid - 1').
c. With the modified array boundary in above steps, we make recursive call findMissingElement(array, low, high) to find the missing number.
For more clarity, you may want to check the following diagramatic illustration of the algorithm for the sequence {1,2,3,4,6,7,8}.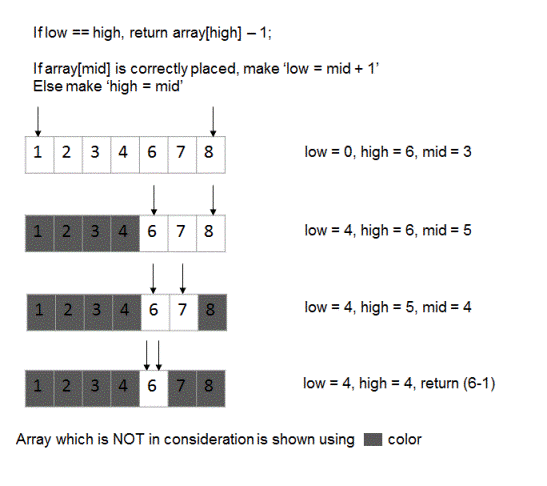
Please feel free to add comments below in case of any queries/feedback.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Finds the missing number in the given increasing sequence from 1 to n using binary search in log(n) time.
* @author Nilesh
*/
public class MissingElementInSortedSequence
{
private boolean correctlyPlaced(int index, int number)
{
// remember we are using 0 based indexing scheme
if (number == (index + 1))
{
return true;
}
return false;
}
/*
* In the given sequence, we search for the first element from the left which is incorrectly placed.
* An incorrectly placed element would not satisfy condition: valueOfElement = index of element + 1.
* Once we find this first incorrectly placed element, we know that the missing number must be equal to
* value of this element minus 1.
*/
private int findMissingElement(int[] array, int low, int high)
{
// Invalid input case: if the array size is 0 or less than 0
if (low > high)
{
System.out.println("Invalid Input");
return -1;
}
// if the last element of the given array is correctly placed, then we can say that
// all the elements of the given array are correctly placed
if (correctlyPlaced(high, array[high]))
{
System.out.println("No missing number. All elements are correctly placed");
return 0;
}
// we have found the first element from the left in the given sequence which is incorrectly placed.
// Missing number must be this element's value minus 1
if (low == high)
{
return array[high] - 1;
}
int mid = (low + high)/2;
/*
* If the middle element is incorrectly placed, we search for the first element in the given sequence
* which is incorrectly placed in the first half(low to mid) of the given sequence. Because array[mid]
* also could be the first element which is incorrectly placed, we need to include that element in the search and
* hence we mark high as 'mid'.
* ---
* If the middle element is correctly placed, we need to search in the second half(mid+1 to high). Note that since
* middle element is correctly placed, we don't need to include array[mid] in the search and hence we mark low as 'mid + 1'
*/
if (!correctlyPlaced(mid, array[mid]))
{
high = mid;
}
else
{
low = mid + 1;
}
return findMissingElement(array, low, high);
}
public int findMissingElement(int[] array)
{
return findMissingElement(array, 0, array.length-1);
}
public static void main(String[] args)
{
MissingElementInSortedSequence solution = new MissingElementInSortedSequence();
int[] sequence = {1,2,4,5,6,7,8};
System.out.println("The missing number from the above sequence is: " + solution.findMissingElement(sequence));
}
}
Order of the Algorithm
Time Complexity is O(log(n))
Space Complexity is O(1)
