Sorting Algorithm - Heap Sort
Given an array, sort the array using Heap Sort algorithm.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Heap sort is an in-place comparison sort.
Heap sort is not a stable sort i.e. it does not ensure the order of same array elements after sorting.
Definition:
A max-heap is a complete binary tree in which the value at root is greater than or equal to the values of left and right children of the root and all the heap nodes follow this property.
Since a max heap is a complete binary tree, it can be represented by an array such that:
1. Element at index 0 is the root.
2. For any node of the heap at index i, including the root node (i=0):
Index of Left child = 2*i+1
Index of Right child = 2*i+2
Parent of the node = (i-1)/2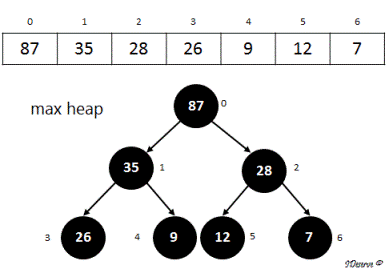
Heap sort algorithm has two steps:
Step 1. Build Max Heap: Convert the array to a max heap.
Call maxHeapify on all internal nodes. For this we start with the last internal node upto the root. The index of the last internal node will be the index of parent of last leaf node which is also the last element in the array.
maxHeapify(array, i, heapSize) - Get larger of current node (element at index i), left child (element at index 2*i+1) and
right child (element at index 2*i+2) and replace it with the current node (index i).
Recurse for left and right nodes to maintain max heap property.
Step 2: Sorting the array using Max Heap
1. Remove the maximum element from the heap (root) and swap it with the last index of the heap (heapSize) and reduce the heap size by 1.
2. Then adjust heap elements (from index 0 to heap size) to maintain max heap property.
3. Repeat this step for second largest element and so on.
For Example, consider the array:
12, 35, 87, 26, 9, 28, 7
Step 1: Build Max Heap:
1. The array can be considered as following complete binary tree: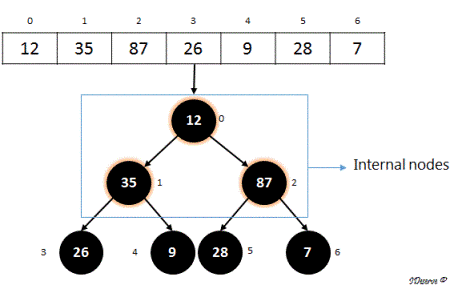
2. Clearly,it is not a max heap. We convert it to a max heap by calling maxHeapify on all internal nodes.
Last internal node
= index of parent of last element of the array
= index of parent of 7 (Index of 7 is 6)
= (6 - 1)/2
= 2
= index of 87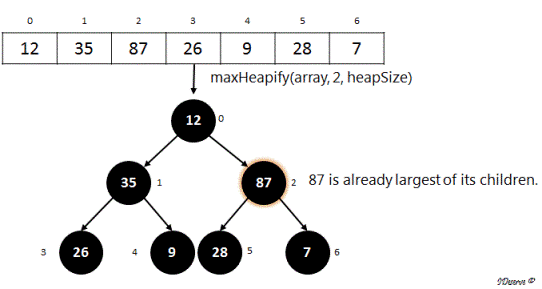
There will be no change in the array on calling maxHeapify(array, 2, heapSize).
Similarly, subtree with root as 35 is also the largest of its children, i.e. satisfies max heap property.
So, there will be no change in the array on calling maxHeapify(array, 1, heapSize) too.
Next we call, maxHeapify(array, 0, heapSize):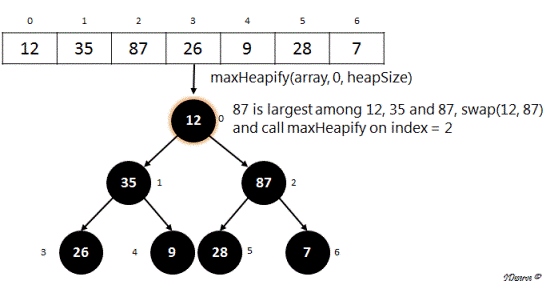
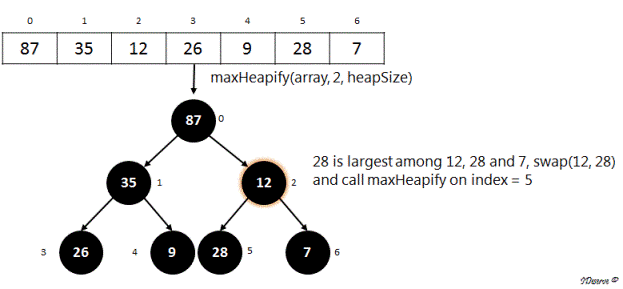
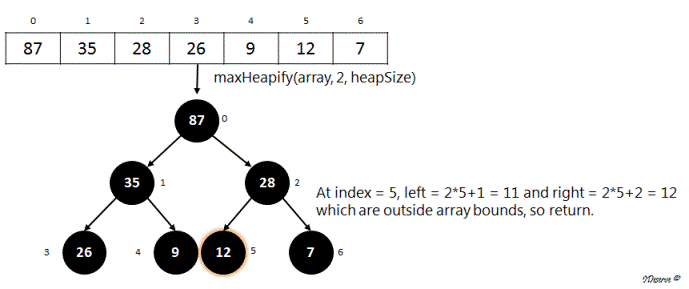
Hence following image shows the max heap created from the array.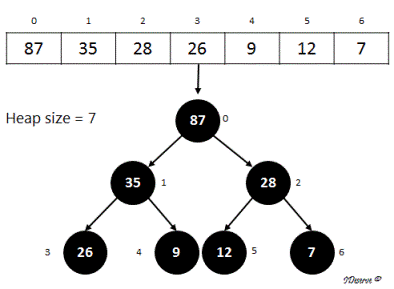
Step 2: Sorting the array using Max Heap created in Step 1
1. Swap max element of the heap (i.e. the root) with the element at last index of the heap.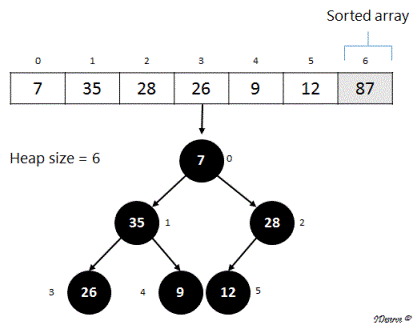
2. Call maxHeapify on the root (index = 0) to maintain max heap property on the remaining heap. Proceeding like before, we get the following heap: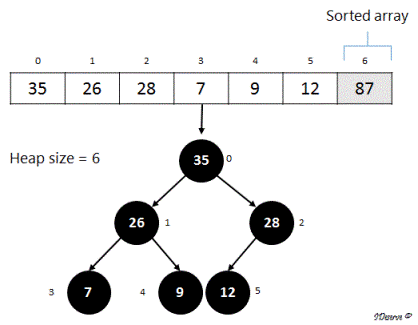
3. Next swap max element of the heap (root) with the element at last index of the heap.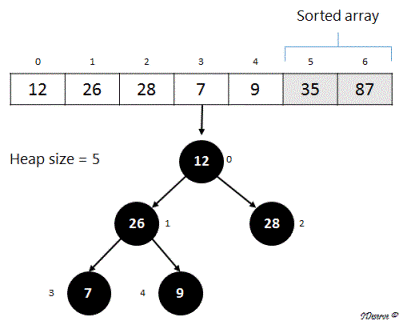
4. Again, call maxHeapify on the root (index = 0) to maintain max heap property on the remaining heap.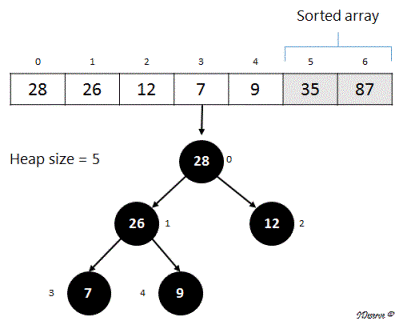
In the next step, 28 (root) will be swapped with 9 (last element in heap) moving 28 to its correct position in the sorted array.
Continuing like this, we can see that the array is getting sorted from max element to smallest element using the max heap.
After applying #1 and #2 of step 2 on the array till heapSize becomes 0, we will get the sorted array as:
[7, 9, 12, 26, 28, 35, 87]
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
import java.util.Arrays;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given an array, sort the array using Heap Sort algorithm.
*
* @author Saurabh
*/
public class HeapSort {
public static void maxHeapify(int[] array, int curIndex, int heapSize){
// Left child in heap
int left = 2*curIndex+1;
// Right child in heap
int right = 2*curIndex+2;
int largest = curIndex;
if(left < heapSize && array[left] > array[curIndex]) {
largest = left;
}
if(right < heapSize && array[right] > array[largest]) {
largest = right;
}
if(largest != curIndex){
swap(array, curIndex, largest);
maxHeapify(array, largest, heapSize);
}
}
public static void buildMaxHeap(int[] array, int heapSize){
// call maxHeapify on all internal nodes
int lastElementIndex = array.length - 1;
int parentIndex = (lastElementIndex - 1)/2;
for(int i = parentIndex; i >= 0; i--){
maxHeapify(array, i, heapSize);
}
}
public static void heapSort(int[] array){
if(array == null || array.length < 2)
return;
buildMaxHeap(array, array.length);
int heapSize = array.length;
for(int i = array.length - 1; i > 0; i--){
swap(array, 0, i);
heapSize = heapSize - 1;
maxHeapify(array, 0, heapSize);
}
}
public static void main(String[] args) {
int[] array = {12, 35, 87, 26, 9, 28, 7};
System.out.println("Original Array:\t\t" + Arrays.toString(array));
heapSort(array);
System.out.println("Sorted Array:\t\t" + Arrays.toString(array));
}
private static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
Order of the Algorithm
Time Complexity is O(nlogn)
Space Complexity is O(1)
