Remove all the half nodes from a given binary tree
Given a binary tree, write a program to remove all the half nodes from it. For example, in the following binary tree, nodes 3,6,2,5 are half nodes.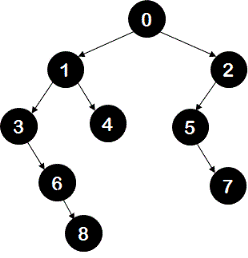
and removing them results in the following binary tree. 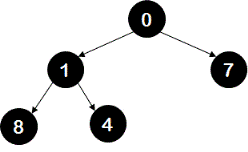
Our program should return the root of the modified binary tree. Note that leaf nodes have both children as null and therefore they should not be removed.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The algorithm uses bottom-up approach to delete the half nodes from the given binary tree. It uses post-order traversal - when first removeHalfNodes(TreeNode currentNode) call is made with currentNode as root of the binary tree, the function uses following steps.
1. If currentNode is null return null since this is a empty tree. This is the base case for this recursive algorithm.
2. Remove all the half nodes from currentNode's left sub-tree and make currentNode'e left child point to this modified left sub-tree. This is done using recursive call - currentNode.left = removeHalfNodes(currentNode.left).
3. Remove all the half nodes from currentNode's right sub-tree and make currentNode'e right child point to this modified right sub-tree. This is done using recursive call - currentNode.right = removeHalfNodes(currentNode.right).
4. Finally when left and right sub-trees are modified for currentNode, check if currentNode's left child is null with right child being non-null value. If this is the case then we need to delete currentNode. We do that by returning currentNode's right child to its parent and making currentNode as null.
5. Similarly, if currentNode's right child is null with left child being a non-null value, we need to delete currentNode. We do that by returning currentNode's left child to its parent and making currentNode as null.
For example,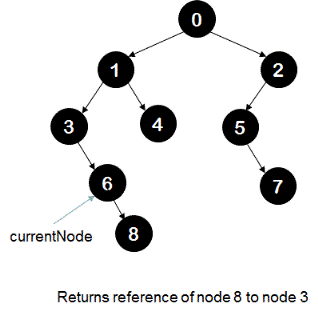
In the above tree when currentNode is 6, it returns reference of node 8 to its parent that is node 3 makes reference of itself as null. Modified tree looks like following tree.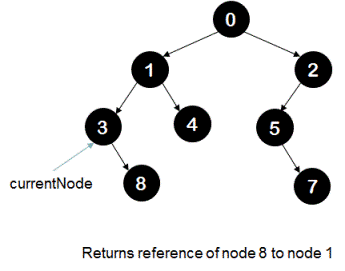
Then again when currentNode is node 3, it again returns reference of node 8 to its parent that is node 1 and modified tree looks like following.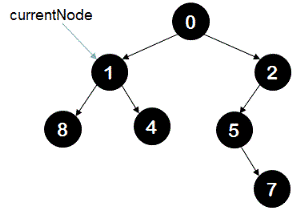
Since this is essentially a post-order traversal, time taken is O(n) and extra space taken is O(1).
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Remove all the half nodes in O(n) time using post-order traversal.
* @author Nilesh
*/
public class RemoveHalfNodes
{
class QueueNode
{
TreeNode node;
int level;
QueueNode(TreeNode node, int level)
{
this.node = node;
this.level = level;
}
}
class TreeNode
{
TreeNode left;
TreeNode right;
int data;
public TreeNode(int x)
{
this.data = x;
}
}
TreeNode root;
/*
0
1 2
3 4 5
6 7
8
*/
private TreeNode createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.right = n6;
n5.right = n7;
n6.right = n8;
return root;
}
public void printLevelOrder()
{
if (root == null) return;
LinkedList<QueueNode> queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentQueueNode = queue.remove();
if (currentQueueNode.level > maxLevelVisited)
{
System.out.print("\n Level-" + currentQueueNode.level + ": ");
maxLevelVisited = currentQueueNode.level;
}
System.out.print(currentQueueNode.node.data + " ");
if (currentQueueNode.node.left != null)
{
queue.add(new QueueNode(currentQueueNode.node.left, currentQueueNode.level + 1));
}
if (currentQueueNode.node.right != null)
{
queue.add(new QueueNode(currentQueueNode.node.right, currentQueueNode.level + 1));
}
}
}
private TreeNode removeHalfNodes(TreeNode currentNode)
{
if (currentNode == null)
{
return null;
}
currentNode.left = removeHalfNodes(currentNode.left);
currentNode.right = removeHalfNodes(currentNode.right);
if (currentNode.left == null && currentNode.right != null)
{
currentNode = currentNode.right;
}
if (currentNode.right == null && currentNode.left != null)
{
currentNode = currentNode.left;
}
return currentNode;
}
public void removeHalfNodes()
{
removeHalfNodes(root);
}
public static void main(String[] args)
{
// TODO Auto-generated method stub
RemoveHalfNodes tree = new RemoveHalfNodes();
/*
0
1 2
3 4 5
6 7
8
*/
tree.createTree();
tree.printLevelOrder();
tree.removeHalfNodes();
/*
0
1 7
8 4
*/
System.out.print("\n\n modified tree after half node removals");
tree.printLevelOrder();
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
