Find the size of largest BST in a binary tree
Given a binary tree, write a program to find the size of largest binary search tree(BST) in it. For example, in the below shown tree, the size of the largest BST is 3. The sub-tree which is rooted at node 15 is a valid BST and has 3 nodes in it.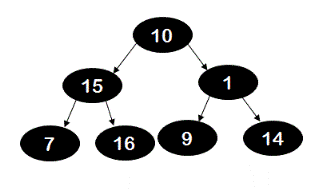
Similarly, in the below shown tree, the size of the largest BST is 5. The sub-tree rooted at node 12 is a valid BST and has 5 nodes in it.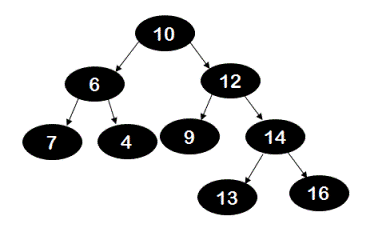
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Method 1: One of the naive approaches to solve this problem could be that 1. Check if tree with current node as root is a valid BST and if it is then return its size. 2. If tree with current node as its root is not a valid BST, then make recursive calls to left and right sub-trees and return the maximum of values returned by these recursive calls. Condition for valid BST could be checked by creating inorder array and checking if it is sorted.
The worst case time complexity of above algorithm is O(n^2) which occurs when the binary tree is skewed one with each node having only right child which is less than its parent.
Method 2: Now let's look at the algorithm which runs in O(n) time. The basic idea used here is that for a tree with root as currentNode to be a valid BST, it's left and right sub-trees have to be valid BSTs, value of currentNode has to be greater than the maximum valued node from its left sub-tree and value of currentNode has to be less than the minimum valued node from its right sub-tree.
To check for above conditions, we return value of maximum valued node, minimum valued node and boolean variable stating if the tree is valid BST or not from every sub-tree. We also return size of a sub-tree if it is a valid BST or return -1 if it is not a valid BST. Using these returned variables from left and right sub-trees, we can check at the currentNode if the tree with its root as currentNode is a validBST or not. If the tree is a valid BST, we calculate size of tree using (1+sizeOfLeftSubtree +sizeOfRightSubtree) and return that along with other variables stated above. If it is not a valid BST we return -1 along with other variables.
Below diagram illustrates returned values from each sub-tree. 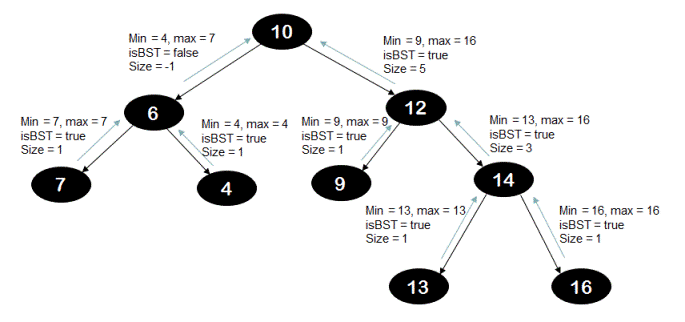
Please checkout function findSizeOfLargestBST(TreeNode currentNode, int[] min, int[] max, boolean[] isBST, int[] maxBSTSize) in code snippet for complete implementation details.
The time complexity of this algorithm is O(n) with O(1) auxiliary space usage.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Finds size of the largest BST in given binary tree. Runs in O(n) time.
* @author Nilesh
*/
public class SizeLargestBST
{
class TreeNode
{
TreeNode left;
TreeNode right;
int data;
public TreeNode(int x)
{
this.data = x;
}
}
TreeNode root;
private int minimum(int a, int b)
{
if (a < b) return a;
return b;
}
private int maximum(int a, int b)
{
if (a > b) return a;
return b;
}
/*
10
6 12
7 4 9 14
13 16
*/
private TreeNode createTree()
{
this.root = new TreeNode(10);
TreeNode n1 = new TreeNode(6);
TreeNode n2 = new TreeNode(12);
TreeNode n3 = new TreeNode(7);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(9);
TreeNode n6 = new TreeNode(14);
TreeNode n7 = new TreeNode(13);
TreeNode n8 = new TreeNode(16);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n2.right = n6;
n6.left = n7;
n6.right = n8;
return root;
}
private int findSizeOfLargestBST(TreeNode currentNode, int[] min, int[] max, boolean[] isBST, int[] maxBSTSize)
{
min[0] = Integer.MAX_VALUE;
max[0] = Integer.MIN_VALUE;
if (currentNode == null)
{
isBST[0] = true;
return 0;
}
// in this call, min[0] and max[0] would be updated
// isBST[0] would be updated if left sub-tree is BST
int leftTreeSize = findSizeOfLargestBST(currentNode.left, min, max, isBST, maxBSTSize);
// check if left sub-tree is a BST and no node in left sub-tree is greater than current node
boolean isLeftValid = isBST[0] && (max[0] < currentNode.data);
// before updating min[0] and max[0] in right sub-tree save min and max values seen so far
int tempMin = minimum(currentNode.data, min[0]);
int tempMax = maximum(currentNode.data, max[0]);
// in this call, min[0] and max[0] would be updated
// isBST[0] would be updated if right sub-tree is BST
int rightTreeSize = findSizeOfLargestBST(currentNode.right, min, max, isBST, maxBSTSize);
// check if right sub-tree is a BST and no node in right sub-tree is less than current node
boolean isRightValid = isBST[0] && (currentNode.data < min[0]);
// before returning update min[0] which would be the minimum value seen in this sub-tree with root as currentNode
// and update max[0] which would be the maximum value seen in this sub-tree before
min[0] = minimum(tempMin, min[0]);
max[0] = maximum(tempMax, max[0]);
// if this tree with root as currentNode is a valid BST
if (isLeftValid && isRightValid)
{
// this sub-tree at currentNode is also a BST
isBST[0] = true;
// update max BST size accordingly
if ((1 + leftTreeSize + rightTreeSize) > maxBSTSize[0])
{
maxBSTSize[0] = (1 + leftTreeSize + rightTreeSize);
}
return (1 + leftTreeSize + rightTreeSize);
}
// if this tree is not BST, we don't really use the value returned by it. Return -1.
isBST[0] = false;
return -1;
}
public void findLargestBST(int[] maxBSTSize)
{
int[] min = new int[1];
int[] max = new int[1];
boolean[] isBST = new boolean[1];
findSizeOfLargestBST(root, min, max, isBST, maxBSTSize);
}
public static void main(String[] args)
{
SizeLargestBST solution = new SizeLargestBST();
/*
10
6 12
7 4 9 14
13 16
*/
solution.createTree();
int[] maxBSTSize = new int[1];
solution.findLargestBST(maxBSTSize);
System.out.println(maxBSTSize[0]);
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
