Given a sequence of words, group together all anagrams and print them.
Given a sequence of words, print all anagrams together, For example, if given word sequence is ["car", "ape", "meal", "pea", "male", "arc", "lame", "dog"] then output of the program should be -
car, arc
ape, pea
lame, meal, male
dog
Order of groups and order of group members between themselves could be different but group members must be same.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This algorithm makes use of a trie data structure for efficient grouping of anagrams. You might want to visit previous posts for more details about a trie data structure,constructing a trie, insertion and search algorithms, its comparison with other data structures etc.
The basic idea used is simple. Insert the individual words of the sequence in a trie but before inserting a word sort it according to the characters. This way, when anagrams are inserted into a trie, their path from root node to leaf node would be exactly the same and if we store the indices of the words in given sequence at leaf node, then we would be able to print all anagrams in grouped manner. The idea is illustrated in below trie diagram for input sequence {"car", "ape", "meal", "pea", "male", "arc", "lame", "dog"}.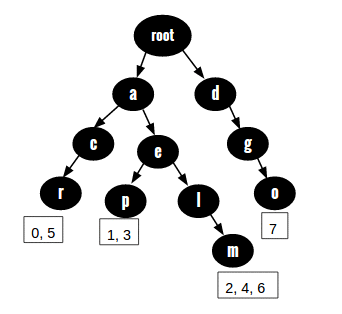
Let's go through an example to understand this idea better. Say we are inserting first word "car" in the trie. First we sort it according to characters. Sorted word would be "acr". Then we insert this sorted word in trie. We also pass the index of the word in given sequence to trie-insert function. Because the word "car" is at 0th index in given sequence, using trie-insertion algorithm, when complete word is inserted, we add index 0 to the list of indices present at the leaf node(at the end of path "root->a->c->r"). Now when we want to insert word "arc" which is at 5th index, we pass the pair ("acr", 5) to trie-insert function. Insertion function then traverses path ("root->a->c->r") and at the node 'r', adds value 5 to the index list. Note that now index list at node 'r' at level-3 has indices 0 and 5 in it implying the presence of anagrams at these indices in given sequence. In similar fashion, this algorithm groups all anagrams together. To print out these groups, all we need to do is store the leaf node and its associated index list in hashmap and once algorithm execution is complete, print out the word groups by using these hashmap stored indices.
The time complexity of this algorithm is O(m.nlogn) where m is total number of words in given sequence and n is the average length of each word in given sequence.
Please checkout code snippet for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.Iterator;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Pattern matching using Trie data structure.
* @author Nilesh
*/
public class TrieForGroupingAnagrams {
// we are only dealing with keys with chars 'a' to 'z'
final static int ALPHABET_SIZE = 26;
class TrieNode
{
ArrayList<Integer> anagramIndices;
TrieNode[] children;
TrieNode()
{
children = new TrieNode[ALPHABET_SIZE];
this.anagramIndices = new ArrayList();
}
}
TrieNode root;
TrieForGroupingAnagrams()
{
this.root = new TrieNode();
}
private int getIndex(char ch)
{
return ch - 'a';
}
public void insertIntoTrie(String key, int index, HashMap anagramNodes)
{
// null keys are not allowed
if (key == null) return;
key = key.toLowerCase();
TrieNode currentNode = this.root;
int charIndex = 0;
while (charIndex < key.length())
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
System.out.println("Invalid Key");
return;
}
if (currentNode.children[childIndex] == null)
{
currentNode.children[childIndex] = new TrieNode();
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
if (charIndex == key.length())
{
currentNode.anagramIndices.add(index);
anagramNodes.put(currentNode, currentNode.anagramIndices);
}
return;
}
public void printGroupedAnagrams(String[] sequence)
{
HashMap<TrieNode, ArrayList<Integer>> anagramNodes = new HashMap();
for (int i = 0; i < sequence.length; i++)
{
char[] charSequence = sequence[i].toCharArray();
Arrays.sort(charSequence);
insertIntoTrie(new String(charSequence), i, anagramNodes);
}
Iterator<ArrayList<Integer>> mapItr = anagramNodes.values().iterator();
while (mapItr.hasNext())
{
ArrayList<Integer> currentAnagramList = mapItr.next();
for (int j = 0; j < currentAnagramList.size(); j++)
{
int indexIntoSequence = currentAnagramList.get(j);
System.out.print(" " + sequence[indexIntoSequence]);
}
System.out.println("");
}
}
public static void main(String[] args)
{
TrieForGroupingAnagrams tr = new TrieForGroupingAnagrams();
String[] sequence = {"car", "ape", "meal", "pea", "male", "arc", "lame", "dog"};
tr.printGroupedAnagrams(sequence);
}
}
Order of the Algorithm
Time Complexity is O(m.nlogn) where m is total number of words in given sequence and n is the average length of each word in given sequence.
Space Complexity is Worst case : O(m*n)
