Longest Prefix Matching using Trie
Given a dictionary of words and an input string, find out the longest prefix of the input string which is also present in the given dictionary.
For example, if dictionary consists of following words -
word, cat, cam, name
And if the input string is 'camera', then output should be 'cam'. If the input string is 'cataract', output should be cat.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This algorithm uses trie data structure for efficient longest prefix matching. You might want to visit previous posts for more details about trie data structure,constructing a trie, insertion and search algorithms, its comparison with other data structures.
An example trie data structure for following (key, value) pairs
("cat",9),("cam",1),("word",5),("name",8)("na",2), ("nam",5).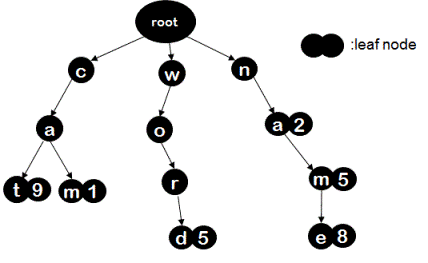
First step of this algorithm is to construct a trie by inserting words of the given dictionary in it. Once this trie is constructed, we just need to traverse along the trie by taking out characters of the input string one by one. During this traversal, we keep track of the characters of the string that have been matched and update the longest prefix matched when a leaf node of trie is visited. Algorithm terminates if it comes across a null TrieNode during traversal or if the complete input string is matched. Null TrieNode visit indicates that there are no more nodes to visit in this path.
Let's run through an example for more clear understanding. Say we are given input string as "camera" and a dictionary with words - cat, cam, word, name, na, nam. We have chosen to use words which are keys in above shown trie. The step by step execution of the algorithm goes as follows for input string "camera"
1. Initialize charSequenceMatched and longestPrefixMatched to empty strings. Go to root node of the trie.
2. Make currentNode = root.children[getIndex('c')]. getIndex('c') would return 2 in the alphabet system of 'a'-'z'.
3. currentNode is now pointing to node 'c' at level-1. Update charSequenceMatched to string "c". Read the next character of the input string that is 'a' and update currentNode = currentNode.children[getIndex('a')].
4. currentNode is now pointing to node 'a' at level-2. Update charSequenceMatched to string "ca". Read the next character of the input string which is 'm' and update currentNode = currentNode.children[getIndex('m')].
5. currentNode is now pointing to node 'm' at level-3. Update charSequenceMatched to string "cam". This node is leafNode, longestPrefixMatched is updated to charSequenceMatched that is "cam". Read the next character of the input string which is 'e' and update currentNode = currentNode.children[getIndex('e')].
6. At this point, currentNode is null and hence the algorithm terminates and returns longestPrefixMatched which is "cam".
Please checkout code snippet and algorithm visualization section for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Longest prefix matching using trie data structure.
* @author Nilesh
*/
public class TrieForLongestPrefixMatch {
// we are only dealing with keys with chars 'a' to 'z'
final static int ALPHABET_SIZE = 26;
final static int NON_VALUE = -1;
class TrieNode
{
boolean isLeafNode;
int value;
TrieNode[] children;
TrieNode(boolean isLeafNode, int value)
{
this.value = value;
this.isLeafNode = isLeafNode;
children = new TrieNode[ALPHABET_SIZE];
}
public void markAsLeaf(int value)
{
this.isLeafNode = true;
this.value = value;
}
public void unMarkAsLeaf()
{
this.isLeafNode = false;
this.value = NON_VALUE;
}
}
TrieNode root;
TrieForLongestPrefixMatch()
{
this.root = new TrieNode(false, NON_VALUE);
}
private int getIndex(char ch)
{
return ch - 'a';
}
public void insert(String key, int value)
{
// null keys are not allowed
if (key == null) return;
key = key.toLowerCase();
TrieNode currentNode = this.root;
int charIndex = 0;
while (charIndex < key.length())
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
System.out.println("Invalid Key");
return;
}
if (currentNode.children[childIndex] == null)
{
currentNode.children[childIndex] = new TrieNode(false, NON_VALUE);
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
// mark currentNode as leaf
currentNode.markAsLeaf(value);
}
public String matchLongestPrefix(String str)
{
if (str == null) return null;
TrieNode currentNode = root;
String longestMatchedWord = "";
String charSequenceTraveled = "";
int charIndex = 0;
while ((charIndex < str.length()))
{
if (currentNode == null) break;
currentNode = currentNode.children[getIndex(str.charAt(charIndex))];
if (currentNode != null)
{
charSequenceTraveled += str.charAt(charIndex);
if (currentNode.isLeafNode)
{
longestMatchedWord = charSequenceTraveled;
}
}
charIndex += 1;
}
return longestMatchedWord;
}
public static void main(String[] args)
{
TrieForLongestPrefixMatch tr = new TrieForLongestPrefixMatch();
tr.insert("word", 5);
tr.insert("name", 8);
tr.insert("cat", 9);
tr.insert("cam", 1);
System.out.println(tr.matchLongestPrefix("camera"));
}
}
Order of the Algorithm
Time Complexity is O(n) where n is the length if the string
Space Complexity is O(n*m) where m is total number of keys in trie and n is average length of a key in trie.
