Check if a binary tree is a binary search tree
Given a binary tree, check if it is a binary search tree (BST).
A binary search tree is a binary tree defined recursively as follows:
1. Root has value greater than all the nodes on its left sub tree
2. Root has value less than all the nodes on its right sub tree
3. Left subtree and right sub tree are also binary search trees
For example: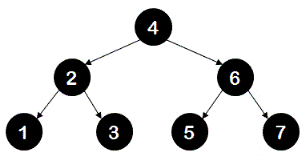
Binary trees which are not binary search trees: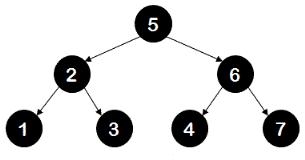
Reason: 4 is on right sub tree of root (5) but is smaller than the root.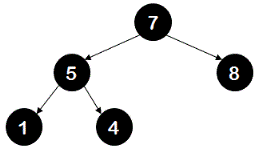
Reason: Left subtree of 7 is not a BST.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Method 1:
1. Find the maximum value in the left sub tree of the root. If it is greater than root, return false.
2. Find the minimum value in the right sub tree of the root. If it is less than root, return false.
3. Recursively check the same for left and right sub trees.
Time complexity: O(n^2)
Method 2:
In a BST, the root is greater than all nodes of the left sub tree. So root value forms an upper bound on left sub tree values.
Similarly, since the root is less than all the nodes of the right sub tree, root value forms a lower bound on the right sub tree values.
This can be used for checking if a binary tree is a binary search tree or not.
1. Initialize, low = MIN_VALUE, high = MAX_VALUE.
2. If root.data <= low || root.data >= high, return false.
3. Recursively check for left sub tree and right sub tree.
a. For left sub tree, pass high as root.data because for a BST, root forms an upper bound for left sub tree node values.
b. For right sub tree, pass low as root.data because for a BST, root forms a lower bound for right sub tree node values.
Time complexity: O(n)
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh.checkbst;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Check if a binary tree is a binary search tree
*
* @author Saurabh
*/
public class Tree {
private Node root;
/*
* Create a sample tree
* 4
* 2 6
* 1 3 5 7
*/
public void createSampleTree() {
root = new Node(4, new Node(2, new Node(1), new Node(3)), new Node(6,new Node(5), new Node(7)));
}
// Efficient method to find if a binary tree is a BST
public boolean isBinarySearchTree() {
return isBinarySearchTree(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
private boolean isBinarySearchTree(Node root, int low, int high) {
if(root == null) {
return true;
}
if(root.data <= low || root.data >= high) {
return false;
}
return isBinarySearchTree(root.left, low, root.data) &&
isBinarySearchTree(root.right, root.data, high);
}
// Simple method that checks if max value in left sub tree is smaller than current node and min value in right sub tree is greater than the current node, for every node of the tree.
public boolean isBinarySearchTreeSimple() {
return isBinarySearchTreeSimple(root);
}
private boolean isBinarySearchTreeSimple(Node root) {
if(root == null) {
return true;
}
if(root.left != null) {
int max = getMaxValue(root.left);
if(max > root.data) {
return false;
}
}
if(root.right != null) {
int min = getMinValue(root.right);
if(min < root.data) {
return false;
}
}
if(!isBinarySearchTreeSimple(root.left) || !isBinarySearchTreeSimple(root.right)) {
System.out.println("");
return false;
}
return true;
}
private int getMinValue(Node root) {
if(root == null) {
return Integer.MAX_VALUE;
}
return min(root.data, getMinValue(root.left), getMinValue(root.right));
}
public int getMaxValue(Node root) {
if(root == null) {
return 0;
}
return max(root.data, getMaxValue(root.left), getMaxValue(root.right));
}
private int max(int n1, int n2, int n3) {
if(n1 > n2 && n1 > n3) {
return n1;
} else if(n2 > n1 && n2 > n3) {
return n2;
} else {
return n3;
}
}
private int min(int n1, int n2, int n3) {
if(n1 < n2 && n1 < n3) {
return n1;
} else if(n2 < n1 && n2 < n3) {
return n2;
} else {
return n3;
}
}
public static void main(String[] args) {
Tree tree = new Tree();
tree.createSampleTree();
System.out.println(tree.isBinarySearchTree());
}
}
class Node {
int data;
Node left;
Node right;
public Node(int data) {
this.data = data;
}
public Node(int data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
}
