Check if a binary tree is balanced or not
Write a program to check if the given binary tree is height balanced or not.
A binary tree is called a height balanced binary tree if it satisfies following conditions -
1. If at any given node, absolute difference of height of left sub-tree and height of right sub-tree is not greater than 1.
2. For any given node, left sub-tree and right sub-tree that node are balanced binary trees themselves.
In the following diagram,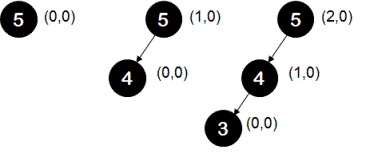
leftmost tree and middle tree, both are height balanced but the rightmost tree is unbalanced. For the rightmost tree, height of left sub-tree at node 5 is 2 and height of right subtree at the same node 5 is 0.
Similarly, below shown tree is height balanced.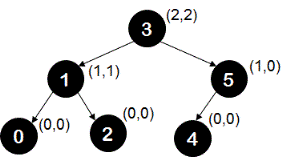
For the below shown tree, sub-tree rooted at node 3 is unbalanced, making the complete tree unbalanced.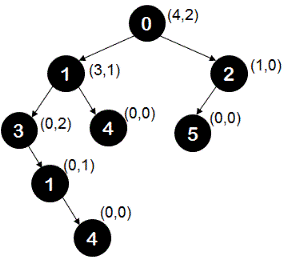
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This algorithm is basically a modified post-order traversal where we first check that for a given node, if the left sub-tree is height balanced, then we check if the right sub-tree is height balanced and finally we check if the tree is balanced at the current node itself. In this algorithm, to indicate that the tree is not balanced at the current node to the calling function, we return value -1. In case the tree rooted at the current node is height balanced, we return the height of tree rooted at current node to the calling function. This height would then be used by calling function to determine height balance at its level. The height of the tree rooted at current node is calculated as: 1 + maximum of(height of left sub-tree, height of right sub-tree)
Let's look at the steps involved in this recursive algorithm. If a call is made to function checkBalance(currentNode) then -
1. If currentNode is null, return height as 0. This indicates that a null tree is balanced with height of 0. This would be the base case for this algorithm.
2. We check if left sub-tree is balanced by making a recursive call: leftSubtreeHeight = checkBalance(currentNode.left)
If left sub-tree is not balanced, we return -1 to indicate that the tree rooted at currentNode is unbalanced as well.
3. We check if right sub-tree is balanced by making a recursive call: rightSubtreeHeight = checkBalance(currentNode.right)
If right sub-tree is not balanced, we return -1 to indicate that the tree rooted at currentNode is unbalanced as well.
4. If both left and right sub-trees are balanced, we check the balance of the tree at the currentNode by checking absolute difference of leftSubtreeHeight and rightSubtreeHeight. If it is greater than 1, then we return -1 to indicate imbalance.
5. If the tree is balanced at the currentNode as well, then we return height of the tree at the currentNode by returning (Math.max(leftSubtreeHeight, rightSubtreeHeight) + 1).
Check out function checkBalance(TreeNode currentNode) in the code snippet for implementation.
Time complexity of this algorithm is O(n) in worst case.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* O(n) solution to check if binary tree is balanced or not. Uses Post-order traversal.
* @author Nilesh
*/
public class CheckIfBalancedBinaryTree
{
class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
0
1 2
3 4 5
6 7
8
*/
private TreeNode createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.right = n6;
n5.right = n7;
n6.right = n8;
return root;
}
// this function returns height of tree rooted at currentNode if the tree is balanced
// otherwise it returns -1
private int checkBalance(TreeNode currentNode)
{
if (currentNode == null)
{
return 0;
}
// check if left sub-tree is balanced
int leftSubtreeHeight = checkBalance(currentNode.left);
if (leftSubtreeHeight == -1) return -1;
// check if right sub-tree is balanced
int rightSubtreeHeight = checkBalance(currentNode.right);
if (rightSubtreeHeight == -1) return -1;
// if both sub-trees are balanced, check the difference of heights
// should be less than or equal to 1
if (Math.abs(leftSubtreeHeight - rightSubtreeHeight) > 1)
{
return -1;
}
// if tree rooted at this node is balanced, return height if tree rooted at this this node
return (Math.max(leftSubtreeHeight, rightSubtreeHeight) + 1);
}
public boolean checkIfBalanced()
{
if (checkBalance(root) == -1)
{
return false;
}
return true;
}
public static void main(String[] args)
{
CheckIfBalancedBinaryTree tree = new CheckIfBalancedBinaryTree();
/*
0
1 2
3 4 5
6 7
8
*/
tree.createTree();
System.out.println("tree is balanced: "+tree.checkIfBalanced());
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
