Check whether a binary tree is a full binary tree or not
Write a program to check if a given binary tree is a full binary tree or not.
A binary tree is a full binary tree if all its nodes have either both children or no children. In other words, if any of its node has only one child then it is not a full binary tree. Both of the following trees are full binary trees.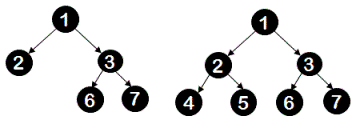
Following two trees are not full binary trees.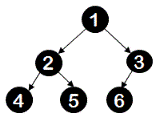
In above tree, node 3 violates the constraint.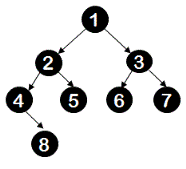
In above tree, node 4 violates the constraint.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
A simple level-order traversal is sufficient to solve this problem. While traversing the tree using level order traversal, if we visit any node with only one child, we return false.
Please checkout code snippet and algorithm visualization section for details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Check if binary tree is full binary tree or not.
* @author Nilesh
*/
public class FullBinaryTreeCheck {
class QueueNode
{
TreeNode node;
QueueNode(TreeNode node)
{
this.node = node;
}
}
class TreeNode
{
TreeNode left;
TreeNode right;
int val;
public TreeNode(int x)
{
this.val = x;
}
}
TreeNode root;
/*
1
2 3
4 5 6 7
*/
private TreeNode createFullBinaryTree()
{
this.root = new TreeNode(1);
TreeNode n1 = new TreeNode(2);
TreeNode n2 = new TreeNode(3);
TreeNode n3 = new TreeNode(4);
TreeNode n4 = new TreeNode(5);
TreeNode n5 = new TreeNode(6);
TreeNode n6 = new TreeNode(7);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n2.right = n6;
return root;
}
/*
1
2 3
4 5 6
7
*/
private TreeNode createNonFullBinaryTree()
{
this.root = new TreeNode(1);
TreeNode n1 = new TreeNode(2);
TreeNode n2 = new TreeNode(3);
TreeNode n3 = new TreeNode(4);
TreeNode n4 = new TreeNode(5);
TreeNode n5 = new TreeNode(6);
TreeNode n6 = new TreeNode(7);
root.left = n1;
root.right = n2;
n1.left = n3;
n1.right = n4;
n2.left = n5;
n3.left = n6;
return root;
}
public boolean checkIfFull()
{
if (root == null) return true;
LinkedList<TreeNode> queue = new LinkedList();
boolean hasLeftChild, hasRightChild;
queue.add(root);
while (!queue.isEmpty())
{
TreeNode currentNode = queue.remove();
hasLeftChild = (currentNode.left != null);
hasRightChild = (currentNode.right != null);
if ((hasLeftChild && !hasRightChild) || (!hasLeftChild && hasRightChild))
{
return false;
}
if (hasLeftChild && hasRightChild)
{
queue.add(currentNode.left);
queue.add(currentNode.right);
}
}
return true;
}
public static void main(String[] args)
{
FullBinaryTreeCheck tree = new FullBinaryTreeCheck();
tree.createNonFullBinaryTree();
System.out.println(tree.checkIfFull());
tree.createFullBinaryTree();
System.out.println(tree.checkIfFull());
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
