Convert a sorted Doubly Linked List to Balanced Binary Search Tree
Given a doubly linked list in sorted order with previous and next nodes. Convert the doubly linked list to a binary search tree with left as previous node and right as next node.
Consider the list below:
The list should be converted to following BST: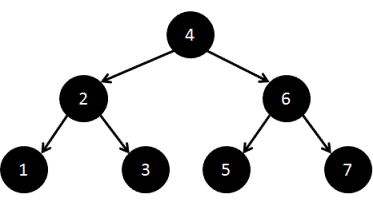
Video coming soon!
Subscribe for more updates
Algorithm/Insights
We recursively traverse to the leaves and then create the tree upwards from the leaves to the root.
Step 1. Calculate the length of the linked list.
Step 2. Recursively create left sub tree from first half nodes.
Step 3. Make middle node as the root and node returned from previous call (Step 2) as left child of the root.
Step 4. Move head to next node.
Step 5. Recursively create the right sub tree from second half nodes.
Step 6. Return root.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Convert a sorted Doubly Linked List to Balanced Binary Search Tree.
*
* @author Saurabh
*/
public class DllToBst {
private ListNode head = null;
private ListNode tail = null;
public void addToList(int data) {
ListNode n = new ListNode(data);
if (head == null) {
head = n;
tail = n;
} else {
// Add to end of list
n.prev = tail;
tail.next = n;
tail = n;
}
}
/**
* Convert DLL to BST:
* prev node will be right child
* next node will be left child
*/
public void convertDllToBST() {
int len = getListLength();
// head is root of BST, tail is null.
head = convertDllToBST(len);
tail = null;
}
private int getListLength() {
int len = 0;
ListNode curr = head;
while (curr != null) {
len++;
curr = curr.next;
}
return len;
}
private ListNode convertDllToBST(int len) {
if (len == 0) {
return null;
}
ListNode left = convertDllToBST(len / 2);
ListNode root = head;
root.prev = left;
head = head.next;
ListNode right = convertDllToBST(len - (len / 2) - 1);
root.next = right;
return root;
}
public void printInorderOrderTraversal() {
printInorderOrderTraversalHelper(head);
}
private void printInorderOrderTraversalHelper(ListNode root) {
if (root == null) {
return;
}
printInorderOrderTraversalHelper(root.prev);
System.out.print(root.data + " ");
printInorderOrderTraversalHelper(root.next);
}
public static void main(String args[]) {
DllToBst dll = new DllToBst();
for (int i = 1; i < 8; i++) {
dll.addToList(i);
}
dll.convertDllToBST();
dll.printInorderOrderTraversal();
}
}
class ListNode {
int data;
ListNode prev;
ListNode next;
public ListNode(int data) {
this.data = data;
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
