Detect a loop in a linked list and find the node where the loop starts.
Given a linked list, detect the starting node for a loop in that list if a loop exists. For example in the following list, loop exists starting at node 2.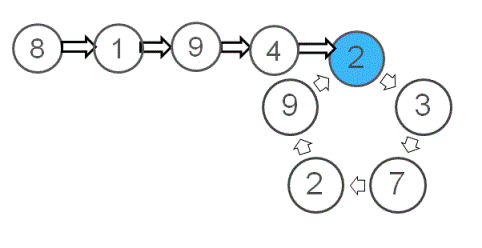
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
This is basically the Floyd's loop detection algorithm.
1. Initialize two references: a slow reference 'S' and a fast reference 'F' to the start of the list
2. Move 'S' forward one node at a time and move 'F' forward two nodes at a time.
3. If at some point of time, reference 'S' and reference 'F' point to the same node of the list then we know that there is a loop in the list otherwise we return null saying there is no loop.
4. After the loop is detected in step #3, we move back reference 'S' to the start of the list again and keep 'F' at same meeting point.
5. Now this time around, we move both 'S' and 'F' forward one node at a time until they meet.
6. The node where they meet is start of the loop.
Why does this work?
Let's look at a simple proof of correctness for above algorithm.
Let 'l' be the length of the loop, 'm' be distance of the start of the loop from beginning of the list and 'k' be the distance of the meeting point of 'S' and 'F' from the start of the loop when they meet for the first time while detecting the loop. 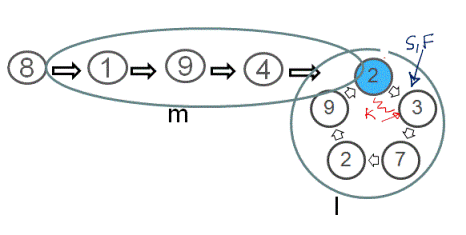
When 'S' and 'F' meet for the first time,
distance travelled by 'S', Dist_S = m + k
and distance travelled by 'F', Dist_F = m + q*l + k ('q' would be an integer >= 1)
Now because 'F' travels twice as fast as 'S',
Dist_F = 2*Dist_S
m + q*l + k = 2(m + k)
(m + k) = q*l which implies (m+k) is an integer multiple of the length of the loop.
After 'S' and 'F' meet at an offset of 'k' links from the start of loop for the first time, we reset reference 'S' to the start of the list while keeping 'F' at same meeting point. Now we move both 'S' and 'F' forward with same speed - one node at a time. When reference 'S' covers distance of 'm' links and reaches at the start of the loop, reference 'F' also covers 'm' links and has reached at an offset of (m+k) links from the start of the loop. As proved earlier, (m+k) is an integer multiple of the length of the loop and therefore 'F' also must have reached at the start of the loop and hence would meet 'S' there. The time complexity of this algorithm is O(n).
Please checkout function findLoopStart() in code snippet for implementation details. Feel free to add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Detect a loop in a linked list and find the node where the loop starts.
* @author Nilesh
*/
public class MyLinkedList
{
private static class node
{
int data;
node next;
node(int data)
{
this.data = data;
}
}
node head;
node tail;
MyLinkedList()
{
}
MyLinkedList(int data)
{
node n1 = new node(data);
this.head = n1;
this.tail = n1;
}
// introduces loop of given length at the end of the list.
public void introduceLoop(int length)
{
if (this.head == null)
{
System.out.println("Empty List. Loop can not be inserted");
return;
}
node p1 = this.head, p2 = this.head;
int count = 0;
while (count < length)
{
if (p2 == null)
{
System.out.println("Incorrect length of the loop given");
break;
}
p2 = p2.next;
count++;
}
node prevP2 = null;
while (p2 != null)
{
prevP2 = p2;
p2 = p2.next;
p1 = p1.next;
}
prevP2.next = p1;
System.out.println("Loop of length " + length + " added starting at node " + p1.data);
}
// finds the node in the list where the loop starts
public node findLoopStart()
{
if (this.head == null)
{
System.out.println("Empty list");
return null;
}
node p1 = this.head;
node p2 = p1;
// Step-1: Loop detection
do
{
if (p1 == null || p2 == null || p2.next == null)
{
System.out.println("No loop found");
return null;
}
p1 = p1.next;
p2 = p2.next.next;
} while (p1 != p2);
// Step-2: Detecting the start of the loop
p1 = this.head;
while (p1 != p2)
{
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
public void addNode_Tail(int data)
{
// if we have an empty list, create a new list and copy its head and tail into
// current object
if (this.head == null)
{
MyLinkedList l_temp = (new MyLinkedList(data));
this.head = l_temp.head;
this.tail = l_temp.tail;
return;
}
// we need to add this node 'n' to the end of the list
node n = new node(data);
node current = this.head, prev = null;
while (current != null)
{
prev = current;
current = current.next;
}
prev.next = n;
this.tail = n; // update the tail info as well
}
public static void main(String[] args)
{
MyLinkedList list = new MyLinkedList();
// 9->1->2->3->4
list.addNode_Tail(9);
list.addNode_Tail(1);
list.addNode_Tail(2);
list.addNode_Tail(3);
list.addNode_Tail(4);
// introduce loop of length 3 at the end of the above list
// the loop would start at node 2
list.introduceLoop(3);
// find where the loop starts
int data = list.findLoopStart().data;
System.out.print("\nloop detected starting at node "+data);
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(1)
