Dijkstra's Shortest Path algorithm
Given a graph with no negative distance between any two nodes, find the shortest distance between initial node '0' and all nodes. For example, for the following graph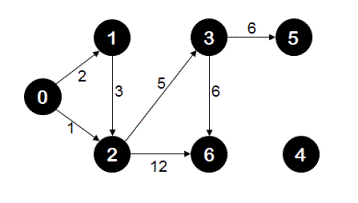
Shortest distance of node '0' from node '0' is 0
Shortest distance of node '1' from node '0' is 2
Shortest distance of node '2' from node '0' is 1
Shortest distance of node '3' from node '0' is 6
Shortest distance of node '5' from node '0' is 12
Shortest distance of node '6' from node '0' is 12
and node '4' is unreachable from node '0'
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
Dijkstra's algorithm essentially uses breadth first search with greedy approach to come up with the shortest distance between given two nodes.
Let the node from which we would find the shortest distance of all other nodes be called initial node. We define the distance of node 'Y' as the distance from the initial node to node 'Y'. Dijkstra's algorithm will assign some initial distance values and will try to improve them step by step. The steps of the algorithm are as following
1. Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes.
This step signifies that at the start of the algorithm, the starting node is at distance 0 from itself and other nodes are unreachable.
2. Set the initial node as current. Mark all other nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
3. For the current node, consider all of its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Also change the parent node of this neighbor as the current node. These parent nodes will help to backtrack the shortest path to a node from the source node. If the currently assigned distance value of the neighbor node is smaller than distance of neighbor from current node + current node's assigned distance then don't do anything.
4. When we are done considering all the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
5. If there is no node remaining in unvisited set or the smallest distance of node in unvisited set is infinity then stop. Algorithm is completed.
6. Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new "current node", and go back to step 3.
(Source: wikipedia)
This algorithm is implemented using priority queue for keeping node with the shortest distance from the source at the front of the queue(remember greedy approach), parent array for keeping track of immediate parent of a node on the shortest path from source to that node, distance array to keep track of shortest distance of a node from source node, unvisted array. Let's see how it works for the graph shown here.
1. To start with, all the nodes are unvisited, distance of all nodes from source node '0' is infinity and parent of all nodes is invalid/-1.
2. Now we add source node '0' to the queue with distance as 0.
3. We remove node 0 from queue, mark it as visited, make distance[0] as 0. Parent[0] still remains -1 since this is the starting vertex. We add neighbors of node 0 that is node 1 and node 2 to the queue, updated their parent to node 0, and update their distance entries as well. 
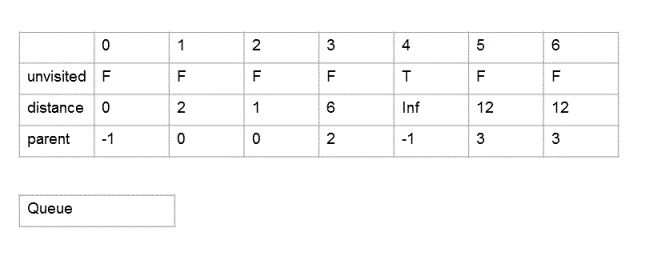
4. Now we remove node 2 from queue which would be at the front of the queue since it has the least distance of all nodes in the queue, mark this node as visited. We then add all the unvisited neighbors of node 2 (node 3 and node 6) to the queue if they are not already in the queue. Then for each unvisited neighbor of node 2 we check if the assigned distance of that neighbor is greater than assigned distance of node 2 + distance between node 2 and that neighbor. If this is the case then we update parent of that neighbor to node 2 and update assigned distance of that neighbor to distance of node 2 + distance between node 2 and that neighbor.
We repeat above step for all entries in the queue until the queue is not empty. As the algorithm progresses, the states of relevant data structures are shown below. At the end of the algorithm, each distance[i] specifies the shortest distance of node 'i' from node 0.
5. 
6. 
7. 
8. 
Please check out the video for step by step illustrative explanation. Feel free to add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.Iterator;
import java.util.PriorityQueue;
public class GraphDijkstra
{
final private static int QUEUE_INITIAL_CAPACITY = 10;
public class QueueNode
{
int nodeId;
int distFromSrc;
public QueueNode(int id, int dist)
{
nodeId = id;
distFromSrc = dist;
}
}
public class queueNodeComparator implements Comparator<QueueNode>
{
@Override
public int compare(QueueNode x, QueueNode y)
{
if (x.distFromSrc < y.distFromSrc)
{
return -1;
}
if (x.distFromSrc > y.distFromSrc)
{
return 1;
}
return 0;
}
}
static private class GraphNode
{
int nodeId;
GraphNode next;
int parentDist;
GraphNode(int id)
{
nodeId = id;
next = null;
}
GraphNode(int id, int dist)
{
nodeId = id;
next = null;
parentDist = dist;
}
}
ArrayList<GraphNode> nodeList;
public GraphDijkstra()
{
nodeList = new ArrayList<GraphNode>();
}
public void addNode(int id)
{
GraphNode node = new GraphNode(id);
nodeList.add(node);
}
public void addEdge(int id1, int id2, int dist)
{
int i = 0;
for (i = 0; i < nodeList.size(); i++)
{
if (nodeList.get(i).nodeId == id1)
{
break;
}
}
if (i == nodeList.size())
{
return;
}
GraphNode node1 = nodeList.get(i);
GraphNode node2 = new GraphNode(id2, dist);
node2.next = node1.next;
node1.next = node2;
}
private GraphNode findGraphNode(int currQueueNodeId)
{
for(int i = 0; i < nodeList.size(); i++)
{
if(nodeList.get(i).nodeId == currQueueNodeId)
{
return nodeList.get(i);
}
}
return null;
}
public void printGraph()
{
for (int i = 0; i < nodeList.size(); i++)
{
GraphNode curr = nodeList.get(i);
while (curr != null)
{
System.out.print(curr.nodeId+"("+curr.parentDist+")"+"->");
curr = curr.next;
}
System.out.print("Null");
System.out.println();
}
}
private void updateQueue(PriorityQueue queue, int nodeId, int oldDist, int newDist)
{
// this step removes the old node with non-optimum distance.
// This is the first step for updating new shortest possible distance
// queue.remove(new QueueNode(nodeId, oldDist));
Iterator<QueueNode> queueItr = queue.iterator();
boolean queueUpdated = false;
while (queueItr.hasNext())
{
QueueNode tempNode = queueItr.next();
if (tempNode.nodeId == nodeId)
{
queueUpdated = true;
tempNode.distFromSrc = newDist;
break;
}
}
// if queue is not updated then that means entry for this node does not exist
// and has to be added now
if (!queueUpdated)
{
queue.add(new QueueNode(nodeId, newDist));
}
}
public int[] findShortestDijkstra (int srcId)
{
Comparator<QueueNode> comparator = new queueNodeComparator();
PriorityQueue<QueueNode> queue = new PriorityQueue<QueueNode>(QUEUE_INITIAL_CAPACITY, comparator);
GraphNode temp = null;
boolean[] unvisited = new boolean[nodeList.size()];
int[] parent = new int[nodeList.size()];
int[] distance = new int[nodeList.size()];
for(int i = 0; i < nodeList.size(); i++)
{
unvisited[i] = true;
parent[i] = -1;
distance[i] = Integer.MAX_VALUE;
}
// add source vertex to the queue with distance as 0
queue.add(new QueueNode(srcId, 0));
// essentially a breadth first logic
while (!queue.isEmpty())
{
// greedy approach -
// remove the first node which would have least distance from source among all the nodes in queue
QueueNode currQueueNode = queue.remove();
unvisited[currQueueNode.nodeId] = false;
distance[currQueueNode.nodeId] = currQueueNode.distFromSrc;
GraphNode currGraphNode = findGraphNode(currQueueNode.nodeId);
GraphNode neighborNode = (currGraphNode == null) ? null : currGraphNode.next;
// for all the neighbors of current graph node, update their distance from source node if applicable
while (neighborNode != null)
{
if (unvisited[neighborNode.nodeId])
{
// and distance from source node through the current node is less than the previous distance
if ((distance[currQueueNode.nodeId] + neighborNode.parentDist) < distance[neighborNode.nodeId])
{
int oldDistance = distance[neighborNode.nodeId];
int newDistance = distance[currQueueNode.nodeId] + neighborNode.parentDist;
distance[neighborNode.nodeId] = newDistance;
parent[neighborNode.nodeId] = currQueueNode.nodeId;
updateQueue(queue, neighborNode.nodeId, oldDistance, newDistance);
}
}
neighborNode = neighborNode.next;
}
}
return distance;
}
public static void main(String[] args)
{
GraphDijkstra graphObj = new GraphDijkstra();
graphObj.addNode(0);
graphObj.addNode(1);
graphObj.addNode(2);
graphObj.addNode(3);
graphObj.addNode(4);
graphObj.addNode(5);
graphObj.addNode(6);
graphObj.addEdge(0,2,1);
graphObj.addEdge(0,1,2);
graphObj.addEdge(1,2,3);
graphObj.addEdge(2,3,5);
graphObj.addEdge(2,6,13);
graphObj.addEdge(3,5,6);
graphObj.addEdge(3,1,6);
graphObj.addEdge(3,6,6);
graphObj.addEdge(5,3,7);
// find the shortest distance of all nodes from node '0'
int[] distance = graphObj.findShortestDijkstra(0);
for (int i = 0; i < distance.length; i++)
{
if (distance[i] == Integer.MAX_VALUE)
{
System.out.println("vertex \'"+ i + "\' is unreachable from vertex '0'");
}
else
{
System.out.println("distance of vertex \'"+ i + "\' from vertex '0' is "+distance[i]);
}
}
}
}
Order of the Algorithm
Time Complexity is O(|E| + |V|^2)
Space Complexity is O(|V|)
