Bellman-Ford Algorithm

Algorithm/Insights

What is meant by Shortest Path?
In a weighted directed graph, shortest path from node A to node B is the path for which the sum of the weights on the edges of the path is minimum of all possible paths from node A to node B.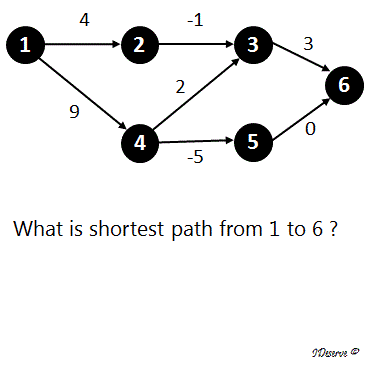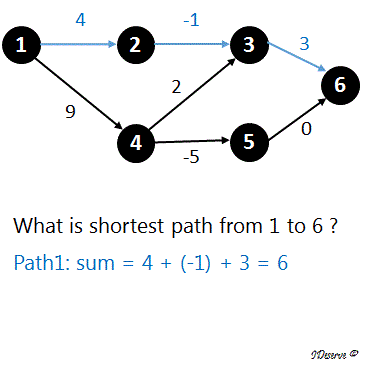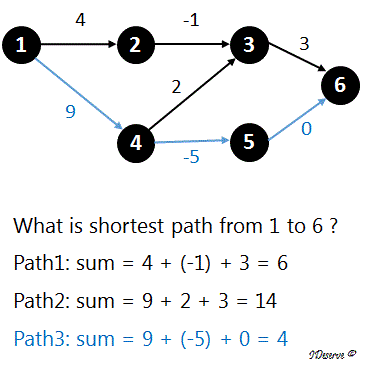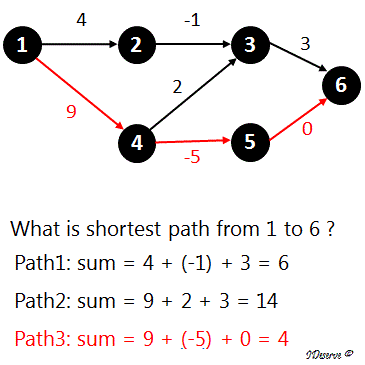


Negative Cycle
If there is a cycle that is reachable from source having negative sum, then any path sum can be decreased further by taking another round of this path. So, no shortest path exists in this case.
For example, consider the following graph: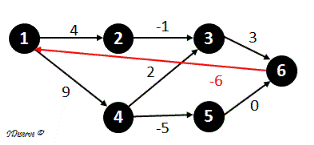

PathSum for 1->4->5->6 = 9 + (-5) + 0 = 4
Here there is a negative cycle 1->4->5->6->1 in the graph that is reachable from source 1
we have path 1->4->5->6->1->4->5->6 with sum = 9 + (-5) + 0 + (-6) + 9 + (-5) + 0 = 4 - 6 + 4 = 2
which is shorter than 1->4->5->6.
Again, we can take another round as 1->4->5->6->1->4->5->6->1->4->5->6
resulting in sum = 9 + (-5) + 0 + (-6) + 9 + (-5) + 0 + (-6) + 9 + (-5) + 0 = 0
which is shorter than previous path.
So there is no shortest path between 1->6.

Bellman-Ford algorithm can detect negative cycles in the graph.

Bellman-Ford Algorithm
G - Graph
s - source vertex
V - vertices in the graph
E - Edges in the graph
(u,v)  - Edge from u to v
distance[i] - shortest distance from source to vertex i
w(u,v) - weight on the edge from u to v

Step 1: Initialize distances from source to all vertices:
    distance[s] = 0
    distance[u] = Integer.MAX_VALUE for all vertices other than s
Step 2: Relax Edges- Repeat following steps V-1 times:
    For every edge E, repeat following steps:
        If distance[v] > distance[u] + weight(u,v) then
            set distance[v] = distance[u] + weight(u,v)
    Consider the example:
    
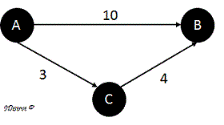
    Source = A
    distance[B] = 10
    distance[C] = 3
    Since distance[C] + w(C,B) = 3 + 4 = 7 < distance[B],
    the alternate path A->C->B is shorter than direct A->B path.
    So, we relax the edge A->B and replace it with A->C->B.
Step 3: Detect negative cycle- Check if there exists an edge (u,v) for which,
    distance[v] > distance[u] + weight(u,v), then graph has a negative cycle.
    So, return true
Step 4: If there is no negative cycle, return false

Code Snippet

			
package com.ideserve.saurabh.questions;

import java.util.ArrayList;
import java.util.List;

class Graph {

	private int V;	// Number of vertices
	private List<Edge> edges; // Edges in the graph

	public Graph(int v) {
		V = v;
		edges = new ArrayList<Edge>();
	}

	public int getV() {
		return V;
	}

	public void setV(int v) {
		V = v;
	}

	public List<Edge> getEdges() {
		return edges;
	}

	public void setEdges(List<Edge> edges) {
		this.edges = edges;
	}
	
	public void addEdge(int u, int v, int w) {
		Edge e = new Edge(u, v, w);
		edges.add(e);
	}
	
}

class Edge {

	private int u; // source vertex
	private int v; // destination vertex
	private int w; // weight on edge from u to v

	public int getU() {
		return u;
	}

	public void setU(int u) {
		this.u = u;
	}

	public int getV() {
		return v;
	}

	public void setV(int v) {
		this.v = v;
	}

	public int getW() {
		return w;
	}

	public void setW(int w) {
		this.w = w;
	}

	public Edge(int u, int v, int w) {
		this.u = u;
		this.v = v;
		this.w = w;
	}

}

public class BellmanFordAlgorithm {

	public static void main(String[] args) {

		Graph g = createTestGraph();
		int distance[] = new int[g.getV()];
		boolean hasNegativeCycle = getShortestPathsBellmanFord(g, 1, distance);
		if(!hasNegativeCycle) {
			for(int i = 1; i < distance.length; i++)
				System.out.println(i + " " + (distance[i] == Integer.MAX_VALUE ? "-" : distance[i]));
		} else {
			System.out.println("No solution found since negative cycle exists in the graph!");
		}
	}

	private static Graph createTestGraph() {
		int v = 7;
		Graph g = new Graph(v);
		g.addEdge(1, 2, 4);
		g.addEdge(1, 4, 9);
		g.addEdge(2, 3, -1);
		g.addEdge(3, 6, 3);
		g.addEdge(4, 3, 2);
		g.addEdge(4, 5, -5);
		g.addEdge(5, 6, 0);		
		
		return g;
	}

	public static boolean getShortestPathsBellmanFord(Graph g, int source, int[] distance) {
		
		int V = g.getV();
		// INITIALIZE: distances from source to all vertices
		for(int i = 1; i < V; i++) {
			distance[i] = Integer.MAX_VALUE;
		}
		distance[source] = 0;
		
		// RELAX EDGES
		for(int i = 1; i < V; i++) {
			for(Edge e: g.getEdges()) {
				int u = e.getU(), v = e.getV(), w = e.getW();
				if(distance[u] != Integer.MAX_VALUE 
						&& distance[v] > distance[u] + w) {
					distance[v] = distance[u] + w;
				}
			}
		}
		
		// DETECT NEGATIVE CYCLE
		for(Edge e: g.getEdges()) {
			int u = e.getU(), v = e.getV(), w = e.getW();
			if(distance[u] != Integer.MAX_VALUE 
					&& distance[v] > distance[u] + w) {
				return true;
			}
		}
		
		return false;
	}
	
}
		

Order of the Algorithm

Time Complexity is O(VE)
Space Complexity is O(V)