Iterative Pre-order Traversal of a Binary Tree
Write a program to traverse the given binary tree in pre-order style without using recursion. For example, for the following tree, output should be 6,4,3,5,9,8. In pre-order traversal, a node is visited first followed by nodes in the left sub-tree which is followed by visit of nodes in the right sub-tree.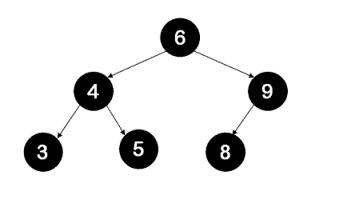
Video coming soon!
Subscribe for more updates
Algorithm/Insights
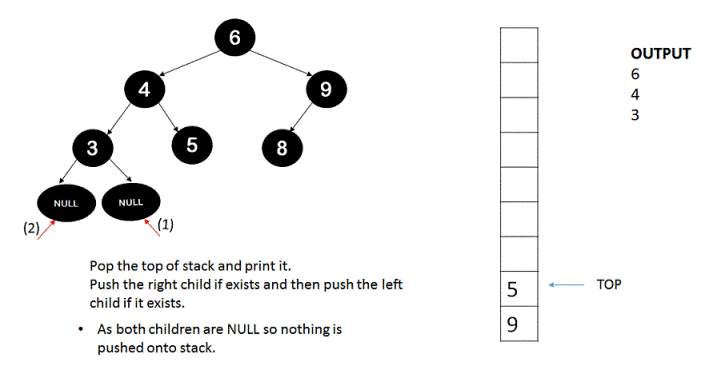
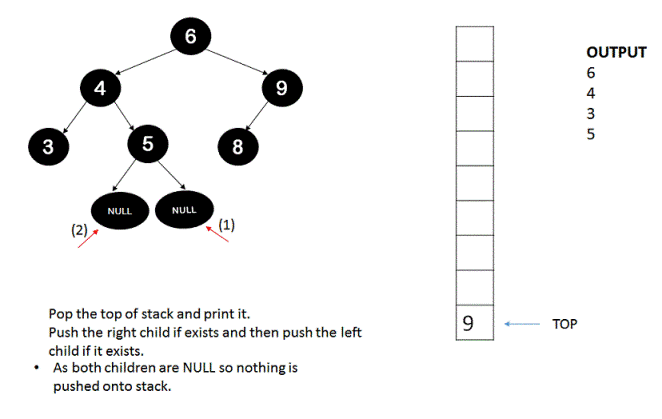
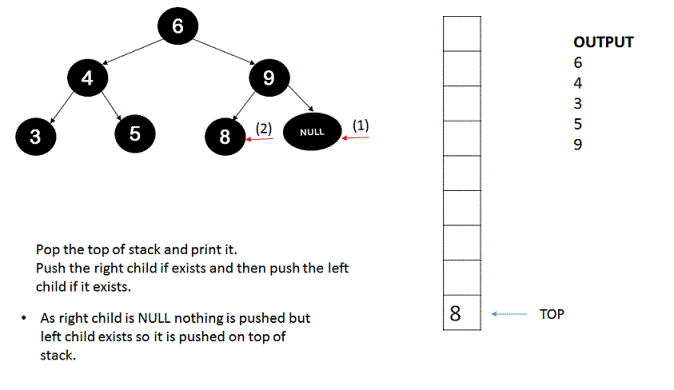
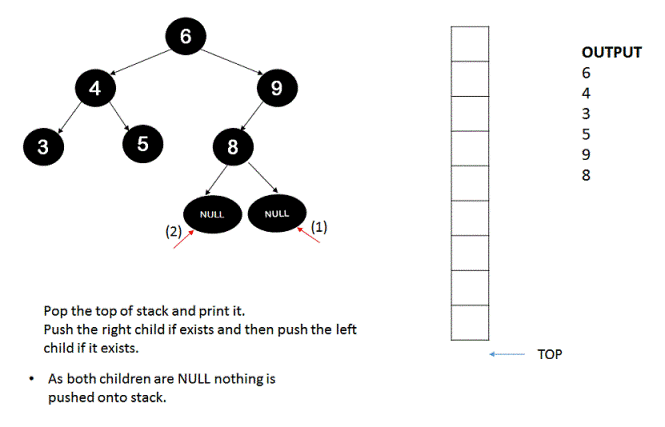
The idea is to basically traverse the tree without recursion and by using stack. Stack is used here in the same way as used in recursion by first pushing the root and then pushing the right child first and then the left child so that left child is processed first because stack follows Last-in-first-out(LIFO) property.
The steps of the algorithm are as following -
1. Push the root of the tree onto the stack.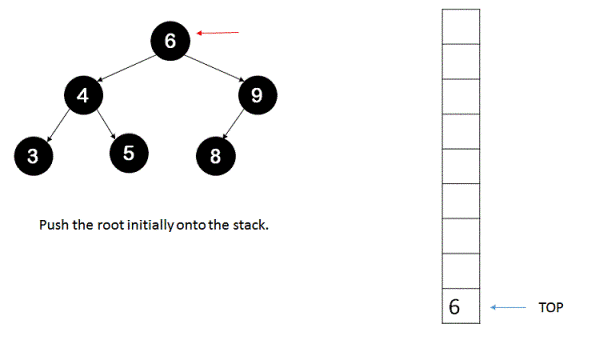
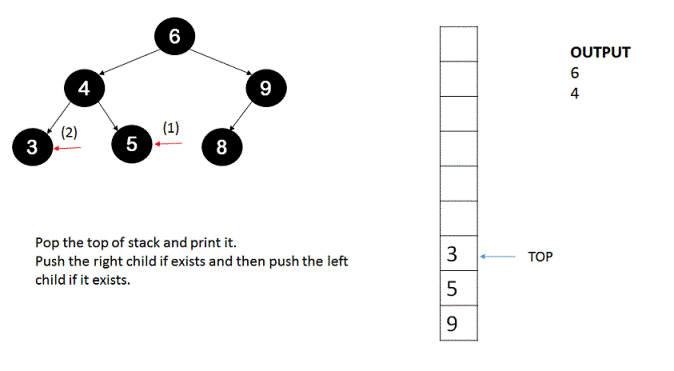
2. Until the stack is empty, keep on popping the top of stack, print it and execute step #3 and step #4.
3. If the top of stack obtained in step #2 has a right child then push it onto the stack.
4. If the top of stack obtained in step #2 has a left child then push it onto the stack.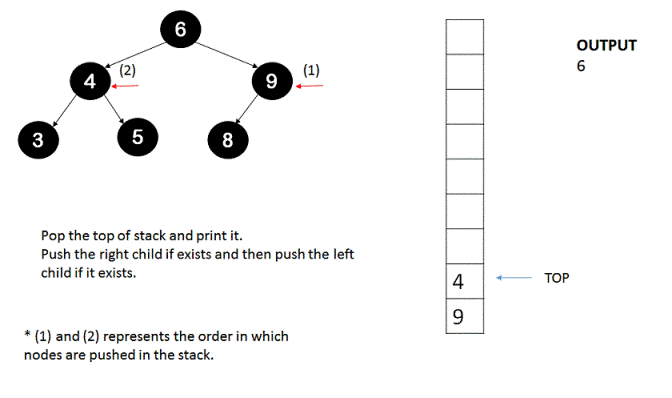

Algorithm Visualization
Code Snippet
package com.ideserve.questions.abhishek;
import java.util.Stack;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Iterative pre-order traversal of a binary tree.
*
* @author Abhishek
*/
public class Tree {
private TreeNode root;
class TreeNode {
private int data;
private TreeNode left;
private TreeNode right;
public TreeNode(int data) {
this.data = data;
}
};
/**
* Method creates a sample tree
* 5
* 4 6
* 3 7 8
*
*/
public void createTree() {
root = new TreeNode(5);
root.left = new TreeNode(4);
root.right = new TreeNode(6);
root.left.left = new TreeNode(3);
root.left.right = new TreeNode(7);
root.right.left = new TreeNode(8);
}
/**
* Method for printing iterative pre-order traversal
* of a binary tree.
*/
public void iterativePreorder() {
TreeNode top;
if (root == null)
return;
Stack<TreeNode> st = new Stack<TreeNode>();
st.push(root);
/*
* Push the root and do the same process as recursive one but in this way:
* a) Print the node's data
* b) Push its right child
* c) Push its left child.
* This is done because stack if LIFO so left child is operated first.
*/
while (!st.empty()) {
top = st.pop();
System.out.print(top.data + " ");
if (top.right != null)
st.push(top.right);
if (top.left != null)
st.push(top.left);
}
}
/**
* Method for testing the algorithm.
*
* @param args
*/
public static void main(String args[]) {
Tree tree = new Tree();
tree.createTree();
tree.iterativePreorder();
}
}
Order of the Algorithm
Time Complexity is O(n) where 'n' is the number of nodes in the tree.
Space Complexity is O(n) as the stack memory is needed for holding maximum 'n' nodes of tree.
