Lowest Common Ancestor of two nodes in a Binary Search Tree
Find Lowest Common Ancestor(LCA) of given two nodes in a Binary Search Tree(BST). The lowest common ancestor (LCA) of two nodes 'n1' and 'n2' in a tree is the lowest(i.e. deepest) node that has both 'n1' and 'n2' as descendants. Each node is considered descendant of itself. So if 'n1' is descendant of 'n2' then LCA of 'n1' and 'n2' would be 'n2' and vice versa (Credits for definition of LCA: Wikipedia).
Let's look at couple of examples to understand definition of LCA more clearly.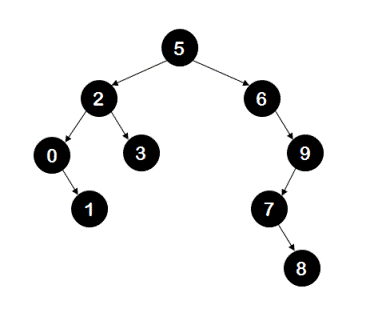
In the above BST,
LCA of nodes '0' and '3' is node '2'.
LCA of nodes '0' and '1' is node '0'.
LCA of nodes '3' and '9' is node '5'.
LCA of nodes '5' and '3' is node '5'.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Idea: Assuming that node 'n1' and node 'n2' exist in the given BST, idea to find LCA is simple. We need to find a node 'n' such that nodes 'n1' and 'n2' are placed on the different sides of node 'n' or either value of node 'n1' or value of node 'n2' is equal to value of node 'n'. For example, 
LCA of nodes '0' and '3' is node '2'. As you can observe node '0' is placed in the left sub-tree of node '2' and node '3' is placed in the right sub-tree of node '2'.
LCA of nodes '0' and '1' is node '0'. This is because node '1' is descendant of node '0'. Hopefully, these examples have helped to get some intuition of how to find LCA. Let's look at the algorithm now.
Algorithm: If the LCA for nodes with values 'v1' and 'v2' is to be found then -
1. First step is to make sure that value 'v1' is less than or equal to value 'v2'. If it is not then we swap 'v1' and 'v2' to make it so.
2. Now knowing that 'v1' < 'v2', we check if nodes with values 'v1' and 'v2' exist in given BST. If node corresponding to either 'v1' or 'v2' is missing then we return -1 indicating LCA could not be found.
3. Say 'n1' be the node found in BST with value 'v1' and 'n2' be the node found in BST with value 'v2'. Now to find LCA of nodes 'n1' and 'n2', we call recursive sub-routine 'findLCA(currentNode = root, n1 = n1, n2 = n2)' which in turn uses following steps:
3a. If 'currentNode' is null then we return LCA as null.
3b. If value of 'n1' < value of 'currentNode' < value of 'n2' then we return 'currentNode' as LCA.
3c. If value of 'currentNode' is either equal to value of 'n1' or 'n2' then we return 'currentNode' as LCA.
Conditions 3a,3b and 3c are base cases for this recursive algorithm. Recursive steps are -
3d. If value of 'currentNode' is greater than values of 'n1' and 'n2', then by using BST property we know that both nodes 'n1' and 'n2' would be in the left sub-tree of currentNode. Hence we search for LCA of 'n1' and 'n2' in the left sub-tree by making a recursive call 'findLCA(currentNode.left, n1, n2)'
3e. Similarly, if value of 'currentNode' is less than values of 'n1' and 'n2', then we search for LCA of 'n1' and 'n2' in the right sub-tree by making a recursive call 'findLCA(currentNode.right, n1, n2)'
Function 'findLCA(int value1, int value2)' in the code snippet has implementation details.
Example:
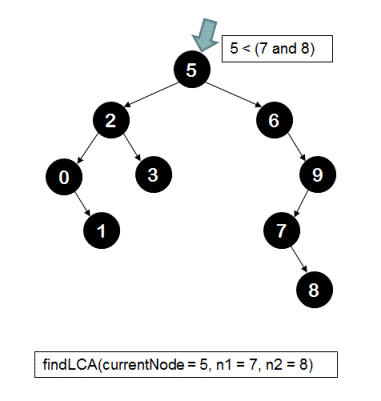
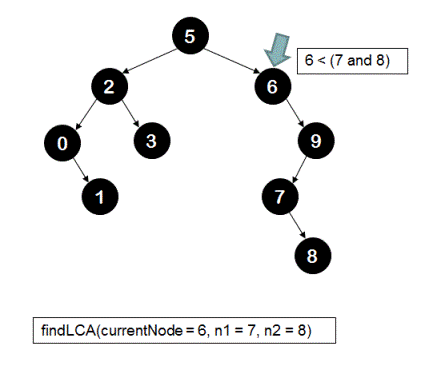
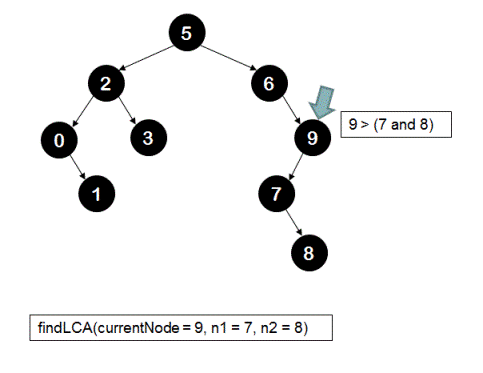
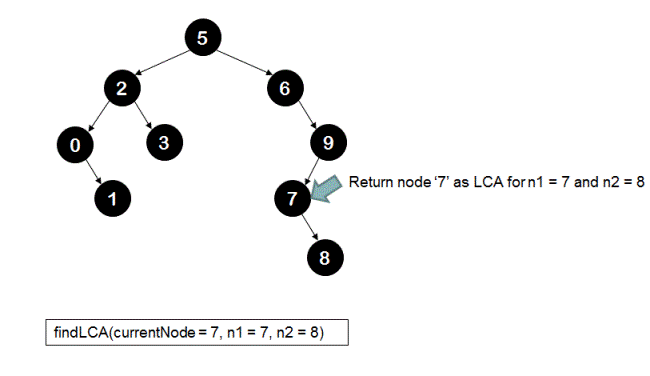
The recursive call sequence for finding the LCA of node '7' and node '8' in the following BST is shown below.
1. 
2. 
3.
4.
The average time complexity of this algorithm is O(log(n)). Worst case could still be O(n) for a skewed BST. The extra space taken is of O(1).
Please add comments in case you have any queries/feedback.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Finds Lowest Common Ancestor(LCA) of two nodes in a Binary Search Tree(BST) in O(log(n)) time.
* @author Nilesh
*/
public class LCAInBST
{
class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
5
2 6
0 3 9
1 7
8
*/
private TreeNode createBST()
{
TreeNode n0 = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
TreeNode n9 = new TreeNode(9);
this.root = n5;
root.left = n2;
root.right = n6;
n2.left = n0;
n2.right = n3;
n6.right = n9;
n0.right = n1;
n9.left = n7;
n7.right = n8;
return root;
}
// finds and returns node with given value in BST
private TreeNode findNode(TreeNode root, int value)
{
if (root == null)
{
return null;
}
if (value == root.value)
{
return root;
}
if (value < root.value)
{
return findNode (root.left, value);
}
else
{
return findNode (root.right, value);
}
}
// the sub-routine that actually finds LCA node for nodes n1 and n2
private TreeNode findLCA(TreeNode currentNode, TreeNode n1, TreeNode n2)
{
if (currentNode == null)
{
return null;
}
// before calling this sub-routine, we have made sure that n1.value <= n2.value
// check if currentNode is the LCA for n1 and n2
if ((n1.value < currentNode.value) && (currentNode.value < n2.value))
{
return currentNode;
}
else if ((n1.value == currentNode.value) || (currentNode.value == n2.value))
{
return currentNode;
}
// if currentNode is not the LCA for n1 and n2
TreeNode lcaNode;
if (n2.value < currentNode.value) // both n1 and n2 are in the left sub-tree of currentNode
{
lcaNode = findLCA(currentNode.left, n1, n2);
}
else // both n1 and n2 are in the right sub-tree of currentNode
{
lcaNode = findLCA(currentNode.right, n1, n2);
}
return lcaNode;
}
// this sub-routine that is entry point for clients and this in turn calls-
// findLCA(TreeNode currentNode, TreeNode n1, TreeNode n2)
public int findLCA(int value1, int value2)
{
// make sure that value1 is always less than or equal to value2
if (value2 < value1)
{
int temp = value1;
value1 = value2;
value2 = temp;
}
// find node corresponding to value1
TreeNode n1 = findNode(root, value1);
if (n1 != null)
{
// find node corresponding to value2
TreeNode n2 = findNode(root, value2);
// find LCA for these nodes
if (n2 != null)
{
TreeNode lcaNode = findLCA(root, n1, n2);
return lcaNode.value;
}
}
// if either n1 or n2 is not found
return -1;
}
public static void main(String[] args)
{
LCAInBST solution = new LCAInBST();
/*
5
2 6
0 3 9
1 7
8
*/
solution.createBST();
System.out.println(solution.findLCA(7, 8));
}
}
Order of the Algorithm
Time Complexity is O(log(n))
Space Complexity is O(1)
