Number of clusters of 1s OR Number of Islands
Given a 2D matrix of 0s and 1s, find total number of clusters formed by elements with value 1. For example, in the below shown 2D matrix there are total three such clusters. 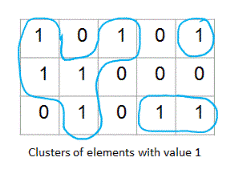
This problem is also known as 'Number of Islands' problem.
Please try solving this problem before jumping on the solution
Click to learn
Subscribe for more updates
Algorithm/Insights
The algorithm to find total number of clusters of elements with value 1 in a given 2D matrix treats the given matrix as a graph and then it finds out total number of connected components in that graph.
While modeling the 'matrix' as a graph -
1. An element matrix[i][j] with value 1 is considered as a vertex.
2. All adjacent elements of matrix[i][j] with value 1 are considered as its neighbor vertices. An element can have maximum of eight neighbors as shown below.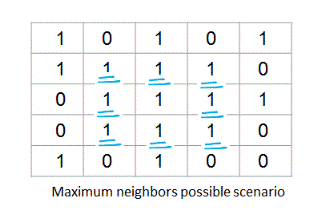
With this graph modeling in place, we use following algorithm to find total number of clusters -
1. Initialize count to 0. Initialize a 2D 'visited' array of booleans which is of size equal to given matrix. Initialize all elements of 'visited' array to false.
2. For an element matrix[i][j], if matrix[i][j] is '1' and visited[i][j] is 'false' then
2a. Increment count by 1.
2b. Start depth first search from element matrix[i][j]. Along with element matrix[i][j], this depth first search would mark all the vertices which are directly or indirectly connected to element matrix[i][j] as visited. In short all the vertices in the cluster starting from vertex matrix[i][j] are visited in this depth first search.
3. Repeat step #2 for all the elements of given 2D matrix.
4. Return the 'count' which is basically total number of clusters of 1s in given 2D matrix.
Time complexity of this algorithm is O(n) where is 'n' is total number of elements in the given 2D array. This algorithm uses O(n) extra space to keep track of visited vertices.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* This problem is also known as 'Number of Islands' problem -
* Treating 2D matrix as a graph and then performing depth first search on that graph,
* this code finds total number of clusters of 1s in given 2D array.
* @author Nilesh
*/
public class NumberOfClusters
{
final static int[] offsets = {-1, 0, +1};
private boolean neighborExists(int[][] matrix, int i, int j)
{
if ((i >= 0) && (i < matrix.length) && (j >= 0) && (j < matrix[0].length))
{
if (matrix[i][j] == 1)
{
return true;
}
}
return false;
}
private void doDFS(int[][] matrix, int i, int j, boolean[][] visited)
{
if (visited[i][j])
{
return;
}
// mark this vertex as visited and visit all its neighbors in depth first manner
visited[i][j] = true;
int xOffset, yOffset;
for (int l = 0; l < offsets.length; l++)
{
xOffset = offsets[l];
for (int m = 0; m < offsets.length; m++)
{
yOffset = offsets[m];
// do not consider vertex[i][j] as its own neighbor
if (xOffset == 0 && yOffset == 0)
{
continue;
}
// check if there exists a vertex at this offset and check if it is '1'
if (neighborExists(matrix, i + xOffset, j + yOffset))
{
doDFS(matrix, i + xOffset, j + yOffset, visited);
}
}
}
}
public int findNumberofClusters(int[][] matrix)
{
// JVM initializes all values to false by default.
boolean[][] visited = new boolean[matrix.length][matrix[0].length];
int count = 0;
for (int i = 0; i < matrix.length; i++)
{
for (int j = 0; j < matrix[0].length; j++)
{
if ((matrix[i][j] == 1) && (!visited[i][j]))
{
// vertex [i][j] marks start of new a cluster. DFS then visits all vertices of this cluster
count += 1;
doDFS(matrix, i, j, visited);
}
}
}
return count;
}
public static void main(String[] args)
{
int[][] matrix = {
{1, 0, 1, 0, 1},
{1, 1, 0, 0, 0},
{0, 1, 0, 1, 1},
};
NumberOfClusters solution = new NumberOfClusters();
System.out.println(solution.findNumberofClusters(matrix));
}
}
Order of the Algorithm
Time Complexity is O(n), 'n': total number of vertices
Space Complexity is O(n)
