Breadth first search in a graph
Given a graph, check if path exists between source node and destination node using breadth first search. In the breadth first search, all nodes at a lower level are visited before all nodes at a higher level. The source node is assumed at level-0, all its neighbors then would be at level-1, neighbors of source node's immediate neighbors would be at level-2 and so on.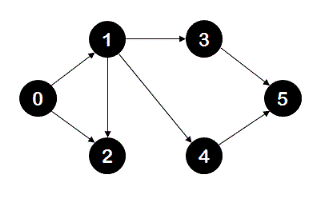
For example, for the above graph, if breadth first search is performed with source node as '0' and destination node as '5', then order of nodes visited would be: level-0 nodes: {0}, level-1 nodes: {1,2}, level-2 nodes: {3,4}, level-3 nodes:{5}. The destination node '5' is found at level-3 and hence breadth first search algorithm should return true. Note that nodes visited at each level are enclosed in set notation to underline the fact that there is no restriction on the order of nodes visited at a particular level.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The algorithm for breadth first search in a graph is a simple queue based traversal algorithm. We will try to understand following steps for doing breadth first search from 'source' node to 'destination' node using an example.
1. Add 'source' node to an empty 'queue', mark 'source' node as visited.
2. While this 'queue' has more nodes -
2a. Remove the first node from this queue. Let's call this currentNode.
2b. If currentNode is 'destination' node, then search is complete. We can return from this point. In the implementation, we have only set boolean 'destNodeFound' as true without returning.
2c. Add all unvisited neighbors of currentNode to queue. While adding each neighbor to queue, mark it as visited. Note that if we add all neighbors of currentNode to queue without checking if it is visited or not, we might end up in never-ending traversal if there are cycles in the graph.
These steps complete the algorithm. In the implementation, we have also kept track of level of current node and maximum level visited so far to identify when the new level starts. Let's look at an example now. For the following graph, if source node is '0' and destination node is '5',
1. Node '0' along with level = 0, is added to an empty queue. Node '0' is also marked as visited. Queue and visited structures look like following: 
2. Queue is not empty, therefore first entry from this queue is removed. currentNode is marked as node 0. And all its unvisited neighbors that is node 1 and node 2 are added to queue. Node 1 and node 2 are also marked as visited. After completion of this step state of queue and visited is shown below: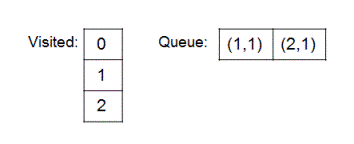
3. Now first entry in this queue is node 1 with level 1. This entry is removed, currentNode is marked as node 1. All its neighbors which are not already visited are added. Newly added neighbors are marked as visited. State of the queue and visited structures is shown below. 
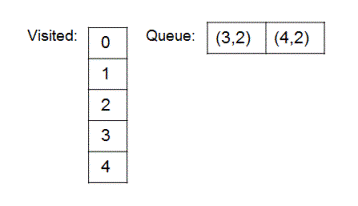
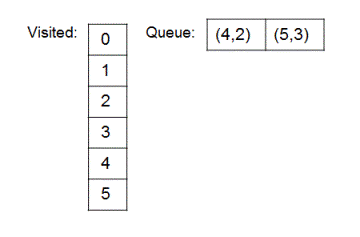
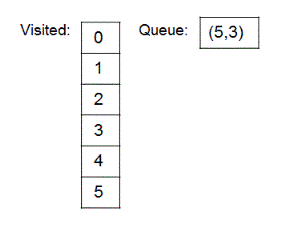
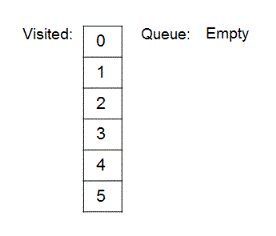
Same step of removal of first entry from queue, marking removed node as the currentNode, adding all unvisited neighbors of currentNode to queue while marking them visited is repeated till the queue become empty. States which 'queue' and 'visited' go through are shown below.
4. 
5.
6.
7.
Adjacency list representation of the graph used in implementation is shown below. Nodelist contains all the nodes in the graph and each node in the nodelist points to a linked list which has all its neighbors.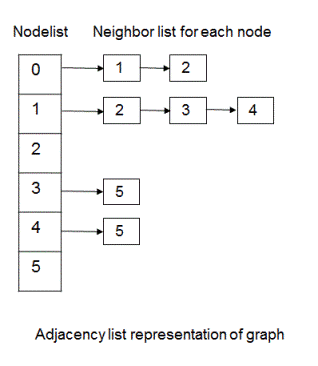
For implementation details, you can check out function breadthFirstSearch(T srcId, T destId). The time complexity of this algorithm is O(|V| + |E|) since every node and every edge would be visited in the worst case.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Breadth first search in a graph to find out if path exists from source node to destination node.
* @author Nilesh
*/
public class Graph<T>
{
private class QueueNode
{
GraphNode graphNode;
int level;
// this constructor is used while doing breadth first traversal
public QueueNode(GraphNode node, int level)
{
this.graphNode = node;
this.level = level;
}
}
private class GraphNode
{
T nodeId;
GraphNode next;
int parentDist;
GraphNode(T id)
{
nodeId = id;
next = null;
}
GraphNode(T id, int dist)
{
nodeId = id;
next = null;
parentDist = dist;
}
}
ArrayList<GraphNode> nodeList;
public Graph()
{
nodeList = new ArrayList<GraphNode>();
}
private void addNode(T id)
{
GraphNode node = new GraphNode(id);
nodeList.add(node);
}
private void addEdge(T id1, T id2, int dist)
{
int i = 0;
for (i = 0; i < nodeList.size(); i++)
{
if (nodeList.get(i).nodeId == id1)
{
break;
}
}
if (i == nodeList.size())
{
return;
}
GraphNode node1 = nodeList.get(i);
GraphNode node2 = new GraphNode(id2, dist);
node2.next = node1.next;
node1.next = node2;
}
// find the node with required nodeId in graph's node list.
private GraphNode findGraphNode(T nodeId)
{
for(int i = 0; i < nodeList.size(); i++)
{
if(nodeList.get(i).nodeId == nodeId)
{
return nodeList.get(i);
}
}
return null;
}
public void printGraph()
{
for (int i = 0; i < nodeList.size(); i++)
{
GraphNode curr = nodeList.get(i);
while (curr != null)
{
System.out.print(curr.nodeId+"("+curr.parentDist+")"+"->");
curr = curr.next;
}
System.out.print("Null");
System.out.println();
}
}
/*
* Does a breadth first traversal of a given graph starting from node with id = srcId.
*/
public boolean breadthFirstSearch(T srcId, T destId)
{
if (nodeList.isEmpty())
{
System.out.println("Empty graph");
return false;
}
// queue used during the traversal
LinkedList<QueueNode> queue = new LinkedList();
// keeps track of node which are visited and added into the queue
HashMap<T, Integer> visited = new HashMap();
// find srcNode with id = srcId in graph
GraphNode srcNode = null;
for (int i = 0; i < nodeList.size(); i++)
{
if (nodeList.get(i).nodeId == srcId)
{
srcNode = nodeList.get(i);
break;
}
}
// if srcNode is not there in graph, breadth first traversal which starts at srcNode cannot be done
if (srcNode == null)
{
System.out.println("Source vertex not found");
return false;
}
boolean destNodeFound = false;
int maxLevelVisited = -1;
// add srcNode in queue, mark it as visited
queue.add(new QueueNode(srcNode, 0));
visited.put(srcNode.nodeId, 1);
while (!queue.isEmpty())
{
QueueNode currentNode = queue.remove();
// if we are now visiting a new level, add new line, update maxLevel visited
if (currentNode.level > maxLevelVisited)
{
System.out.print("\nlevel " + currentNode.level+ "-");
maxLevelVisited = currentNode.level;
}
// print current graph node
System.out.print(currentNode.graphNode.nodeId + " ");
if (currentNode.graphNode.nodeId == destId)
{
destNodeFound = true;
}
// first neighbor of current graph node
GraphNode neighbor = currentNode.graphNode.next;
// add all neighbors of current graph node into the queue
while (neighbor != null)
{
// if this neighbor is not visited earlier, mark it as visited
// add it to the queue at appropriate level
if (visited.get(neighbor.nodeId) == null)
{
visited.put(neighbor.nodeId, 1);
queue.add(new QueueNode(findGraphNode(neighbor.nodeId), currentNode.level + 1));
}
neighbor = neighbor.next;
}
}
return destNodeFound;
}
public static void createGraph(Graph graph)
{
graph.addNode(0);
graph.addNode(1);
graph.addNode(2);
graph.addNode(3);
graph.addNode(4);
graph.addNode(5);
graph.addEdge(0, 1, 2);
graph.addEdge(0, 2, 4);
graph.addEdge(1, 2, 4);
graph.addEdge(1, 3, 5);
graph.addEdge(1, 4, 3);
graph.addEdge(3, 5, 1);
graph.addEdge(4, 5, 1);
}
public static void main(String[] args)
{
Graph<Integer> graph = new Graph();
createGraph(graph);
// prints adjacency list representation of this graph.
// graph.printGraph();
int srcNodeId = 0, destNodeId = 5;
// search destination node from source node using breadth first search
System.out.print("\n\nIf path exists between source and destination node:\n" + graph.breadthFirstSearch(srcNodeId, destNodeId));
}
}
Order of the Algorithm
Time Complexity is O(|V| + |E|)
Space Complexity is O(|V|)
